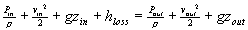
Variable Description: Metric English
P in Pressure at inlet Pa psi
P out Pressure at outlet Pa psi
V in Velocity of fluid at inlet m/s ft/s
V out Velocity of fluid at outlet m/s ft/s
Z in Height of the inlet m ft
Z out Height of the outlet m ft
p Density of the fluid kg/m^3 lbm/m^3
h loss Head loss (losses due to friction) m^2/s^2 ft^2/s^2
Bernoulli's Equation
With regard to a toilet, we can assume that the density (p) of water is constant, gravity (g) is constant, h loss and v_in are both negligible compared to the other terms, and p in is atmospheric pressure. I timed the toilet in my house and it took roughly 10 seconds. Since we know that it takes 8 seconds for 2 gallons of water to flow through the cross sectional area of the pipe, we can determine a rough estimate for the flow rate (Q). Knowing Q and assuming the cross sectional Area, we can estimate the average velocities at specific points.
Flow rate:
Q = A*v
Since the flow rate (Q) is constant throughout the system, according to the law of conservation of mass (m_in = m_out) and assuming that the density (p) remains constant, we can state that:
A*v in = A* v out
P in Pressure at inlet Pa psi
P out Pressure at outlet Pa psi
V in Velocity of fluid at inlet m/s ft/s
V out Velocity of fluid at outlet m/s ft/s
Z in Height of the inlet m ft
Z out Height of the outlet m ft
p Density of the fluid kg/m^3 lbm/m^3
h loss Head loss (losses due to friction) m^2/s^2 ft^2/s^2
Bernoulli's Equation
With regard to a toilet, we can assume that the density (p) of water is constant, gravity (g) is constant, h loss and v_in are both negligible compared to the other terms, and p in is atmospheric pressure. I timed the toilet in my house and it took roughly 10 seconds. Since we know that it takes 8 seconds for 2 gallons of water to flow through the cross sectional area of the pipe, we can determine a rough estimate for the flow rate (Q). Knowing Q and assuming the cross sectional Area, we can estimate the average velocities at specific points.
Flow rate:
Q = A*v
Since the flow rate (Q) is constant throughout the system, according to the law of conservation of mass (m_in = m_out) and assuming that the density (p) remains constant, we can state that:
A*v in = A* v out
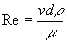
Limiting Characteristics
Factors that may limit the performance of the toilet would include the cross sectional area of the bowl, the amount of water used to flush the toilet, and the time it takes for all the water to pass through. The mechanical efficiency is not that important in the case of the toilet.
Friction:
The friction between water and the siphon pipe is relatively low and can be determined using the Reynolds number.
Where v is the velocity of the fluid, d is the diameter of the pipe the fluid is flowing through, p is the density of the fluid (water=1000 kg/m^3), and m is the viscosity of the fluid (water=1x10-3 kg/m*s). When the Reynolds number is less than 2300, it is considered laminar flow and friction forces are assumed to be negligible.
Factors that may limit the performance of the toilet would include the cross sectional area of the bowl, the amount of water used to flush the toilet, and the time it takes for all the water to pass through. The mechanical efficiency is not that important in the case of the toilet.
Friction:
The friction between water and the siphon pipe is relatively low and can be determined using the Reynolds number.
Where v is the velocity of the fluid, d is the diameter of the pipe the fluid is flowing through, p is the density of the fluid (water=1000 kg/m^3), and m is the viscosity of the fluid (water=1x10-3 kg/m*s). When the Reynolds number is less than 2300, it is considered laminar flow and friction forces are assumed to be negligible.