Calculating the Trajectory of a Launch:

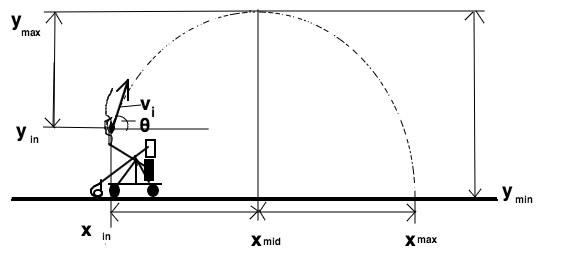
(My Image)

When using a trebuchet, if you ever happen to have one at your disposal, you may be interested in knowing how high and how far the projectile you launch will go... for safety! To get a rough sense of what your trebuchet will do, it is helpful to apply some simple kinematic equations. Using the calculations covered in the launch mechanism section of this site, and with some measurements of the trebuchet, the tangential velocity (vt) can be calculated. With this value and the angle the projectile is launched at (see launch mechanism), you can calculate all that is necessary for a safe launch. The calculations below will give you a sense of the range of the trebuchet, but these numbers will be slightly greater than what happens in reality, this is because air resistance is not taken into account by the kinematic equations used.

Calculations: (The variables reference the diagram above)

(V_{y
mid})² = (V_{y in})² – 2•g•(y_max – y_in)

0 = (V_t•sin( θ)) – 2•g•( y_max – y_in)

y_max = (V_t•sin( θ)) / (19.62) + y_in

V_{y
mid} = V_{y in} – (g•t₁)

0 = V_t•sin( θ) - (9.81•t₁)

t₁ = (V_in•sin( θ)) / (9.81)

(V_{y final})² = (V_{y mid})² + 2•g•(y_max - y_min)

(V_{y final})² = 0 + 19.62(y_max - 0)

V_{y final} = (19.62 • y_max)^1/2

V_{y
final} = V_{y mid} – (g•t₂)

V_{y
final} = 0 + (9.81•t₂)

t₂ = V_{y final} / 9.81

t = t₁+ t₂

x_f = x_in + V_{x in}• t + (½•a_x•t²)

x_f = x_in + V_t•cos( θ)• t + 0

∆x = V_t•cos(θ)• t

V_impact = ((V_{x in})² + (V_{y
final})²)^1/2

To solve for the maximum height the
projectile will reach (solving for only half of
the trajectory, so Vy mid is zero)

Knowing Yin the release height of the
projectile, θ the release angle, and
gravitational acceleration, the max
height in the trajectory can be calculated.

Solved for max height of trajectory.

Finding the time it takes for the projectile to
reach its maximum height.

Because at max height Vy mid is zero.

Solved for time of first half of trajectory.

To compute the time that it takes for the
projectile to complete the second part of its
trajectory, we need to find the final velocity
in the y-direction.

Because Vy mid is zero and ymin is ground
level which we set to zero.

Solve for final velocity in the y direction.

With Vy final we can now find the time it
takes for the projectile to complete the
second part of its trajectory.

Solved for t2.

Add both time segments together to find
the total time the projectile is in motion.

Now, using the time, we can find the range,
the horizontal distance traveled by the
projectile.

ax is zero, because the projectile does
not accelerate in any horizontal direction.

∆x is the range of the projectile.

This equation shows the impact velocity
with which the projectile you launch will
hit the ground.

Now, using the above, you know how high, how far your projectile will go, along with how long it will fly for and how fast it will hit the ground! Remember that these equations are predictions they do not account for many parts of the system, air resistance and uneven ground for instance.

Class Information

University: University of Alaska Fairbanks
Class: General Physics I
Semester: Fall of 2016
Professor: David E. Newman
Student: Riley Bickford

The Trebuchet

Class Information