Launch Mechanism:

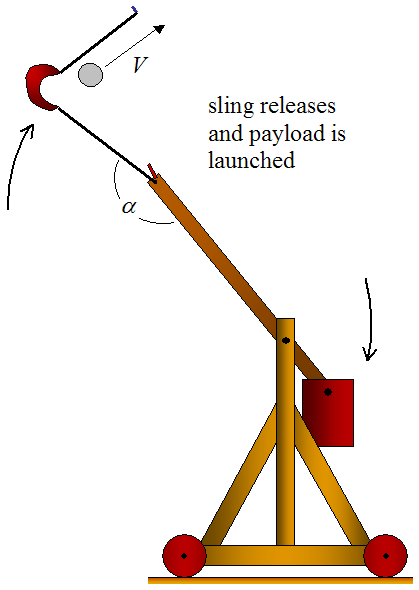
How does the Trebuchet launch objects? To understand this an understanding of the mechanics of the Trebuchet must be grasped first.

Courtesy of Wikipedia

A trebuchet makes use of a simple machine to lift and then drop a massive object in order to launch another smaller object. This simple machine is the lever, which allows one to move a great mass with little effort.

Archimedes moving the earth with
a lever.

Courtesy of nyu.edu

As Archimedes, the renown scientist and inventor of ancient Greece stated "Give me a place to stand, and I will, move the earth" (Archimedes Lever). He is pictured above doing as he said, moving the earth with a lever. Applying a force to a strong and long enough lever with a correctly placed fulcrum can lift massive objects.

The mathematics behind this goes like this:

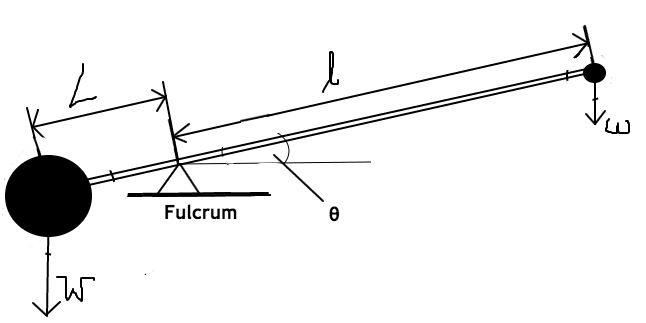(My image)

Assuming the system in the diagram would settle to equilibrium (horizontal position), then the following must be true.

ℓ • (w • sin( θ)) = L • (W • sin(θ))

canceling sin(θ) , we get:

ℓ • w = L • W

From this equation, and knowing that W >> w, and L >> ℓ we see that a smaller force w can in fact lift a greater force W, depending on the exact values and the position of the fulcrum.

With the goal of launching w, W would need to be very large to overcome the mechanical advantage ω has with ℓ be much larger than L . Applying enough force (W) by attaching a great enough mass to the L end of the lever would cause the lever to tilt counter-clockwise causing ω to accelerate in the counter-clockwise direction. This would be how ω would be launched.

Now that we know how the lever works in principle and what conditions would be necessary to launch a mass using one, let us look at the trebuchet itself.

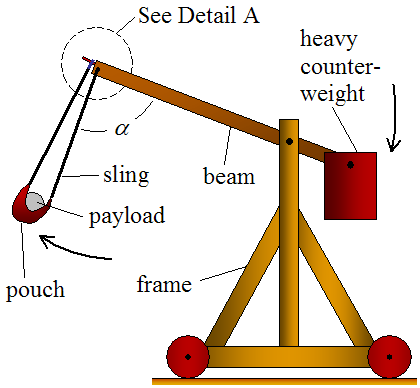
Trebuchet Diagram:

Courtesy of real-world-physics-problems.com

To relate this to the simple explanation of the Fulcrum-Lever system above, we see that the lever is now a wooden beam held up by another beam functioning as its fulcrum in its med-section. The 'heavy counter-weigh' is now the large mass that when released will launch 'payload' (the smaller mass) stored in the pouch. The frame, which supports the fulcrum and the entire system is assumed to be stationary, more on that later.

The arrows on that diagram above show that as the 'heavy counter-weigh' falls the sling carrying the mass is lifted. Assuming the 'heavy counter-weigh' is much larger that the 'payload', the system will turn about the axis of rotation, where the fulcrum and the lever are attached, quite quickly. As ℓ in this case is larger that L, and the beam is rigid, the 'payload will experience a far greater acceleration than the 'heavy counter-weigh' as it is launched. See below for the mathematics behind this, it has to do with the angular acceleration magnified by the contrast in size between ℓ and L.

(My Image)

Calculations:

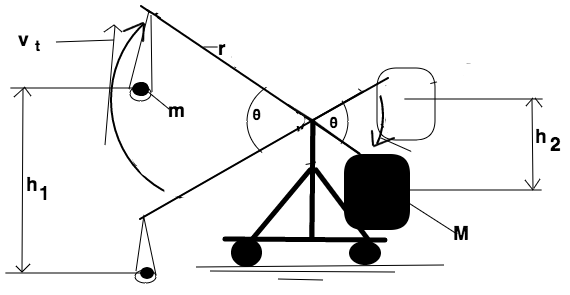
U_g2i + U_g1i + K_2i+ K_1i= K_2f + K_1f +U_g2f + U_g1f

(M•h₂•g )+(m•h_1i•g) +0 +0 = 0+(½•I•(ω )² )+0+(m • h_1f • g)

ω = (2•g•(Mh₂+ mh_1i – mh_1f)/I)^1/2

v_t = ω • r

Conservation of
Mechaical Energy

Expanded into
equations for potential and
kinetic energy

Solved for angular velocity

Converted into final
tangential velocity

M - larger mass

m - smaller mass

ω - angular velocity

h = heights

v_{t - tangential velocity}

r -radius

I - Moment of Inertia this comes from the length of r and the mass of the beam)

g - gravity

*i and f subscripts denote initial and final values

In this manner, using the conservation of mechanical energy and the equations for potential and kinetic energy that follow, we can solve for the final angular velocity which is converted to tangential velocity. Note that conservation of mechanical energy is never entirely true and the calculations above only serve as a model for what occurs in the launching process.

This is what the Trebuchet will look like at the moment that the tangential velocity is calculated:

Courtesy of real-world-physics-problems.com

An assumption made earlier in this article was that none of the energy of the launch resulted in horizontal translation of the trebuchet, despite there being wheels present. Although dissipative forces were not accounted for above, this assumption takes into account friction. To move a body static friction must be overcome, since the trebuchet model has four wheels, and the trebuchet is massive, it is unlikely that it will budge, though not impossible. To figure out if it will budge, see the calculations below.

F_fr= µ _s • N_t

F_fr= (0.62)• (mt • g)

F_fr= 6.08 • mt

Frictional Force is equal to the normal
force of the trebuchet multiplied by the
coefficient of static friction (between
wood and concrete)

Substituting values

Solving for maximum static frictional
force

mt - Mass of Trebuchet

F_fr- Static Frictional Force

g - gravitation acceleration (9.81m/s^2)

N_{t -
Normal force of trebuchet}

µ_s - Coefficient of static friction (wood and concrete)

So for the trebuchet to move, there would have to be a force generated by the launch in any horizontal direction that surpasses the frictional force calculated above.

Click here. To learn about the 'payloads' trajectory, after it's launch.

Class Information

University: University of Alaska Fairbanks
Class: General Physics I
Semester: Fall of 2016
Professor: David E. Newman
Student: Riley Bickford

The Trebuchet

Class Information