
Newton's 2nd Law
|
Newton’s Laws of Motion create the framework to approach a lot of physics concepts within. Newton’s Laws of Motion are: 1st Law: An object in motion will remain in motion, and an object at rest will remain at rest, unless another force counteracts it. 2nd Law: Force= mass*acceleration. The greater the mass, the more force needed to accelerate it. 3rd Law: Every action has an equal and opposite reaction. Newton’s 2nd Law is especially useful when analyzing an object in a dynamic situation. If you can identify all the forces acting upon an object, then you can easily solve for the quantities of unknown variables. To help identify forces acting on an object, a force diagram can be used. A force diagram shows all the forces acting on an object, including the magnitude of the force and the direction. To illustrate, here I will use a move called the splits.
[video from N.
Gyswyt]
 [photo from N. Gyswyt] Here is the same picture, but now
converted into a force diagram. 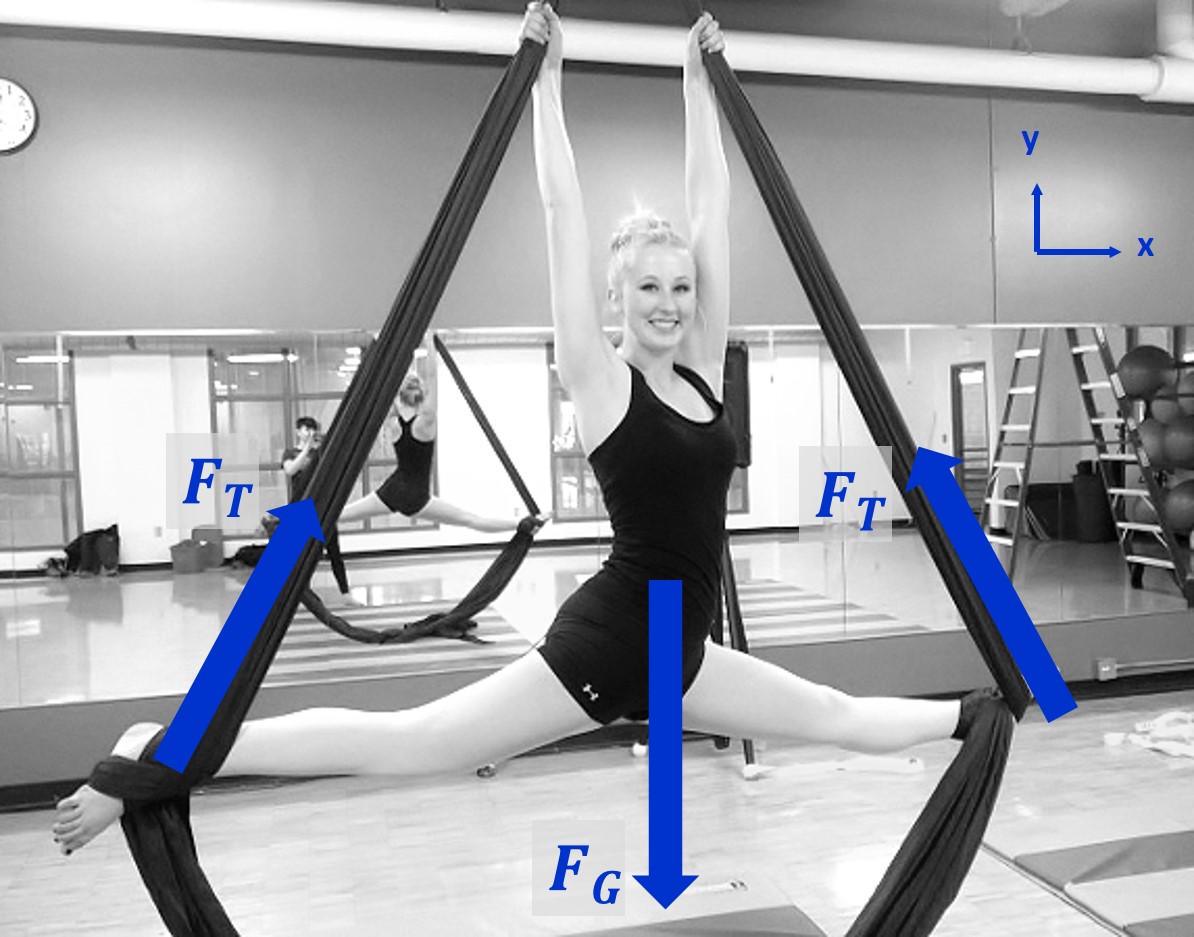 [image from N. Gyswyt] This representation can still be
difficult to understand, especially if a more
complex situation is modeled with more forces
present. The example I am using is more
straightforward, however. A free-body
diagram is the next tool that can be used
to model a dynamic situation. In a free-body
diagram, the object of interest is represented
very simply, often with a dot or a box. Then the
forces are drawn onto the object with their
respective magnitudes and directions. A quantity
that has both magnitude and direction is
referred to as a vector. Here is the
free-body diagram for this example. (I
represented my body as rigid object following
the lines of my legs for simplicity, and am
negating any force my hands play, as that is
simply for balance, I am not supporting a
significant amount of my weight with my hands). 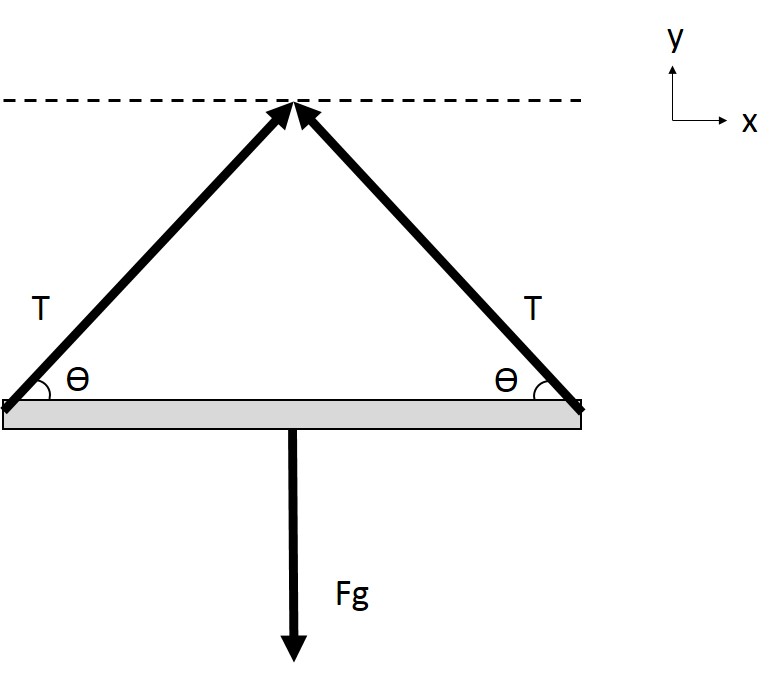 [image from N. Gyswyt] The forces that are acting on the
object of interest are the forces of gravity and
tension. There are two separate force tensions,
but here they are equal and opposite. To solve
for the net force acting on an object,
it is easy to simply sum all the forces in the x
direction and all the forces in the y direction.
To do this, we can break down the force tension
vectors into x and y components. 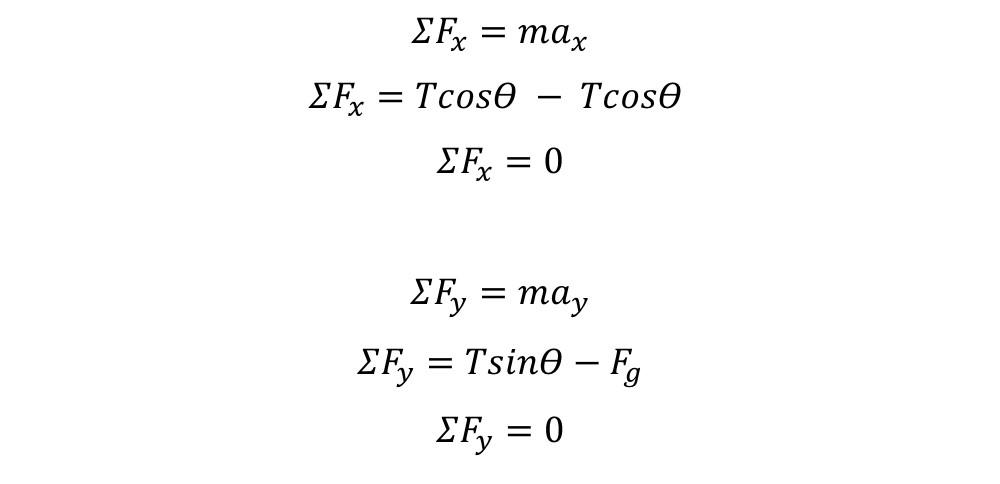 As there is no acceleration in
this situation, my body is not moving in any
direction, the net force is equal to zero. Force
gravity and force tension are still present, but
they are balancing each other out. If one of the
forces was greater, then I would move in the
direction it was applied in. For example, If I
was suspended from a crane instead of the
ceiling, and the crane winched up, force tension
would become greater than force gravity and I
would move in the upwards direction. I can
easily solve for the magnitude of force tension
from these equations though, as long as I know
my mass and the angle of the force vectors.
|
| Homepage |
| Newton's 2nd
Law |
| Friction |
| Conservation
of Energy |
| Rotation |
| Resources |