The Physics of Ice Skating
Home
History
Skate Design
Forces and Motion
Sources
How
is motion achieved?
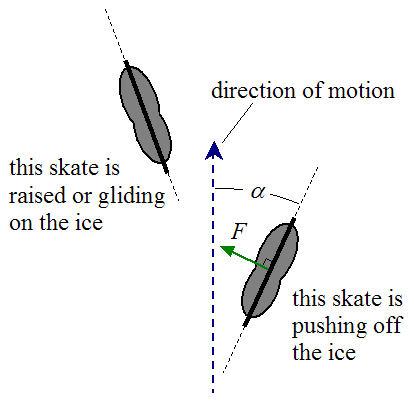
Basic ice skating requires a fairly
simple motion. Forward motion is achieved by
pushing off at an angle using the edge of one
skate. This edge cuts into the ice and provides a
surface that has a higher coefficient of friction.
With other foot the skater glides and then pushes
off on the edge and repeats this motion. A greater
forward acceleration can be accomplished if the
skater pushes the skates at larger angle away from
the intended direction of motion (Normani, 2014).
The diagram below illustrates this motion.
Forces
in Turning
Ice skaters often wish to turn
corners. Hockey players, figure skaters, and speed
skaters usually must all turn corners. Below is a
picture of speed skaters turning a corner at a
high velocity.
For the skater
to turn to the right, they must apply a force to
the left. This works much like driving in a car
around a turn. The car's wheels turn right and the
car pushes down on the road to the left. By
Newton's third law, for every action there is an
equal and opposite reaction. This reaction force
is the road pushing with an equal force on the car
to the right. The net force is to the right so the
car travels in that direction.
This example of the car is similar to the ice
skater turning a corner, except that the ice
skater's center of mass must balance so that the
person does not fall over. The skater therefore
must lean inwards when turning corners. The skates
are turned to the right but the person must also
lean to the right for balance to be kept. The
diagram below shows the basic diagram of what
forces are acting on the person as the right
corner is turned.
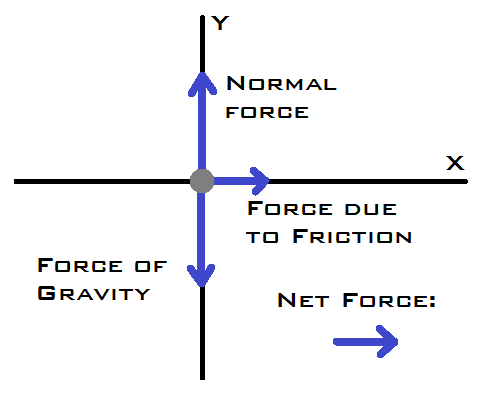
Photo
credit: Lindsey Kromrey
From this basic knowledge of forces when
turning corners many things can be determined.
For example from Newton's second law comes the
equation:
force
= (mass) * (acceleration)
If the skater is staying
at a constant speed but going around a turn
the acceleration can turn into:
acceleration
= (velocity^2) / (radius)
Also
the only force acting on the skater is the
frictional force to the right (see above
diagram). This friction force can be put
in terms of the normal force that the ice
is applying to the skater and the
coefficient of friction that the skates
obtain (from side-to-side not the lower
value when moving forward).
force
= (friction coefficient) * (normal
force)
Since there is no motion up or down, the
normal force will be equal to the
gravitational force which is:
normal
force = (mass) * (acceleration of
gravity)
When combined, this equation is given:
(friction
coefficient) * (mass)
* (acceleration of gravity) = (mass)
* (velocity^2) /
(radius)
The
mass cancels out and the final
equation is:
(friction
coefficient) * (acceleration of
gravity) = (velocity^2) / (radius)
This can be solved for any of the variables
and used to answer questions like:
How great does
the coefficient of friction have to be to
turn at a certain velocity with a certain
radius? or
How fast can the skater go around the
corner without losing their traction?
These questions hold valuable answers for that
can help skaters know their limits. These
evaluations are very valuable to speed skaters
but also apply to figure skaters and hockey
players as well.
|