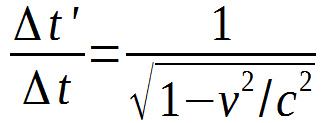Derivation of the Relative Velocity Time Dilation Equation


*The following is an excerpt from Fred Behroozi's "A Simple Derivation of Time Dilation and Length Contraction in Special Relativity" It is just a nice and comprehensive explanation I wanted to include.*

"Consider a simple light clock in its rest frame. The clock consists of two parallel mirrors with a photon bouncing between them (see Fig. 1). The photon’s period of oscillation in its rest frame is

(1) T = 2d/c.

As usual c is the speed of light and d stands for the “proper” distance between the parallel mirrors.





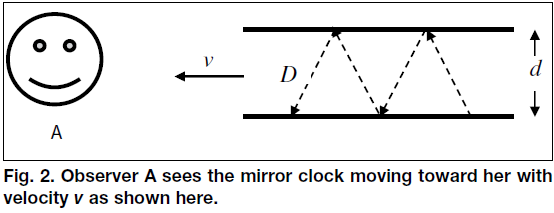
Now let us consider the period of this clock as measured by Observers A and B, each moving with speed v toward the clock as seen in Fig. 1. Each of the two observers carries along a clock identical to the mirror clock for time keeping. Observer A will see the clock moving toward her with velocity v as shown in Fig. 2 and measures the period of the moving clock as the time taken by the photon to bounce up and down between the two mirrors. Let TA be the period of the clock measured by Observer A. Clearly TA is the time the photon takes for a round trip between the two mirrors, which consists of one bounce up and one down. The length of each bounce D (see Fig. 2) is simply the hypotenuse of a right triangle with the sides d and vTA/2. Therefore,

(2) D = [d^2 + (vTA/2)^2]^1/2,

and the round trip time is given by

(3) TA = 2D/c = {2[d^2 + (vTA/2)^2]^1/2}/c
or
(4) TA^2 (1 – v^2/c^2) = 4d^2 /c^2

since by Eq. (1)

(5) 4d^2 /c^2 = T2.

Observer A concludes that the period of the moving clock is

(6) TA = T / (1 – v^2/c^2)^1/2

This is the usual time dilation result. So Observer A concludes that the “moving” clock runs slow compared with his own clock." (Fred Behroozi).

Where equation 6 gives is the equation used in Relative Velocity Time Dilation:




Return to:
Title Page
Relative Velocity Time Dilation