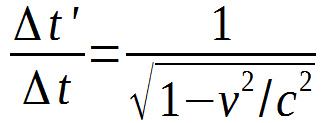Relative Velocity Time Dilation


"Passengers on an 8 hour long airline flight going 920 kmph land having aged 10 nanoseconds less than people on the surface of earth"(Davies). When something is moving faster than something else, time dilation is experienced due to the discrepancy between velocities. The equation used to quantify exactly how much time changes at different speeds is as follows (To see how another physics teacher derived this equation click here):



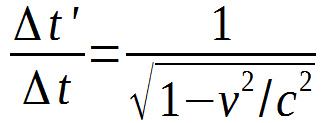
Where:
Δt' = The amount of time that passed in the stationary object's reference frame
Δt = The amount of time that passed in the moving object's reference frame
v = The velocity of the moving object
c = The speed of light

So, for example, if somebody travels on a spaceship going 50% the speed of light for one hour, how much time elapsed for a stationary observer on earth?
Given:

Δt = 1 hour
v = .5c

Find:
Δt'

$Δt' = 1 / sqrt(1-.25c^2/c^2)$
$Δt' = 1 / sqrt(.75)$
$Δt' = 1.1547$

The stationary observer would say that it took the spaceship 1 hour and 9 minutes to cover the distance the spaceship actually traveled in 1 hour.

The above equation can be graphed to show how much time is dilated at various velocities expressed in fractions of the speed of light:


Taken from: http://commons.wikimedia.org/wiki/File:Time_dilation.svg

The graph makes it obvious that for a significant amount of time dilation to be experienced, the velocity must be near the speed of light. At around 86.6% of the speed of light, one hour on the moving object would be equivalent to two hours on the stationary object. At 99.99% of the speed of light, one hour on the moving object would be equivalent to about 71 hours on the stationary object. Time dilation caused by relative velocities can be easily proven experimentally with atomic clocks.

John Matson describes one of these experiments in his article "How Time Flies". "In one landmark test, in 1971, Joseph C. Hafele of Washington University in St. Louis and Richard E. Keating of the U.S Naval Observatory flew cesium atomic clocks around the world on commercial jet flights, then compared the clocks with reference clocks on the ground to find that they had diverged, as predicted by relativity. Yet even at the speed and altitude of jet aircraft, the effects of relativistic time dilation are tiny - in the Hafele-Keating experiment, the atomic clocks differed after their journeys by just tens to hundreds of nanoseconds" (Matson).

With one atomic clock remaining stationary and another moving at any velocity, the one remaining stationary will always tick faster than the one moving, given that they are at the same distance from the center of a gravitational field to ensure that gravitational time dilation is not the culprit.



Next: Gravitational Time Dilation
Previous: What is Time Dilation?
Title Page