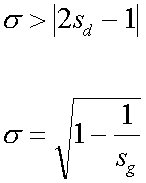The stability triangle
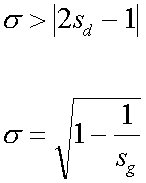
Abbreviations
|
sg
|
Gyroscopic
stability factor |
|
sd
|
Dynamic
stability factor |
Explanations
The dynamic stability condition  can be expressed in an alternate way. leading to a very illustrative interpretation
of bullet stability.
can be expressed in an alternate way. leading to a very illustrative interpretation
of bullet stability.
In using a quantity s,
according to the above definition, the dynamic stability condition takes
a very simple form (see above formula). This means that for a bullet to
be gyroscopically and dynamically stable, a plot of s
vs. sd has to remain completely within the stability
triangle (green area in the figure below).

The red areas are regions of gyroscopic stability but dynamic
instability: either the slow mode oscillation (left area) or the fast mode
oscillation (right area) get umdamped.