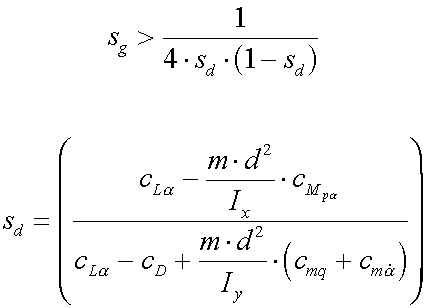
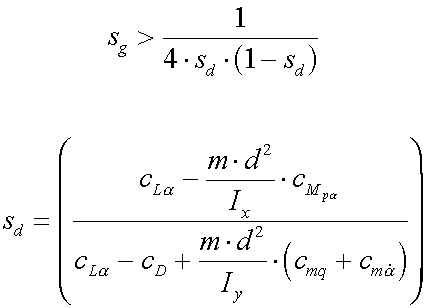
|
|
Drag coefficient |
|
|
Lift coefficient derivative |
|
|
Magnus moment coefficient derivative |
|
|
Pitch damping moment derivative |
|
|
Gyroscopic (static) stability factor |
|
|
Dynamic stability factor |
A dynamic stability factor sd can be defined from
the linearized theory of gyroscopes (assuming only a small angle of yaw)
and the above dynamic stability condition can be formulated. An
alternate formulation of this condition ![]() leads to the illustrative stability triangle.
leads to the illustrative stability triangle.
sd however depends on five aerodynamic coefficients. Because these coefficients are hard to determine, it can become very complicated to calculate the dynamic stability factor, which varies as a function of the momentary bullet velocity.