A Touch of Math Magic

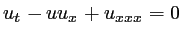
This is the Korteweg-de Vries equation, usually termed the "KdV equation". It was formulated through research conducted in the late 1800s investigating weakly nonlinear shallow water waves. Although this study was not related to Russell's, the equation resulted in modeling a singular wave of positive elevation. It was the same type of wave Russell saw! Above is the generalized (and less scary-looking) form of the equation. It is a third-order nonlinear partial differential equation.

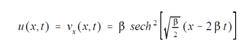
This function is a solution to the equation. In other words, taking the partial derivatives of this function and plugging them into the KdV will equate to zero.

For the first term, derive u(x,t) with respect to t. For the second term, notice that it is composed of two functions multiplied together. This is what makes the KdV nonlinear. So subtract the product of the original function u (x,t) and its derivation with respect to x. By now, maybe you already knew/guessed that the third term is a triple derivation of u(x,t) with respect to x. This is what classifys the KdV as third-order. It's a bit of a lenthy and annoying thing to do by hand. I know this from experience. Yay for MATLAB.

It wasn't until the studies of Zabusky and Kruskal in the 1960s that the term "soliton" was officially used. They were investigating something that initially had nothing to do with solitons. Energy transfer in a crystal lattice structure was hypothesized to be nonlinear. For this to be true, it was predicted that the system would result in thermal equilibrium being reached. But in 1955, Fermi, Pasta and Ulam conducted computer simulations. The results of nonlinear interactions did not, in fact, approach thermal equilibrium in the lattice structure. So Zabusky and Kruskal discovered that the KdV equation could model a sinusoidal initial condition. When applied to the lattice, it breaks into many solitons that "run" around the lattice at different speeds. Their ability to pass through each other enabled them to, at some point as time increases, all collide at essentially the same point. This collision is not exact due to the slight phase shifts after collision, like we discussed on an earlier page. Therefore, a number of solitons came together and nearly resembled initial condition states after a period of time. This explained why nonlinear systems did not reach thermal equilibrium. Solitons were the answer!

I may have lost you there. Okay, say we take my friend's guinea pig and clone him. Now we have 4 and we assume they are physically able to run around the circumference of a giant soccer ball. We'll also assume that they are secretly superheroes and are able to scamper through one another.

If we start them off at the same location on the ball, the fatter ones will run slower. Since all 4 have different masses, they travel at different velocities around the ball. When they pass through each other, they continue on at their same speed and don't change their body structure. BUT their hair gets a little messed up, throwing off their groove, but only a little.

As more time passes, it can be expected that the pigs will all arrive at the same point on the ball at the same time. Would this be their initial condition? No. By the time they arrive here, their hair is an unfortunate mess and their grooves are out of sync.

Therefore, we can see why a series of solitons cannot replicate their initial state exactly. Their phase shifts prevent them from forming the exact same initial state. Also, from this analogy we can see why they do not disperse to result in equilibrium. That would be like expecting the pigs to STRETCH their bodies over the whole circumference. That's a little gross. As I said, they cannot change their body structure, just like how solitons do not change their bell-shaped curve.