Belt/Rope Friction
Imagine that you want to keep a huge tanker from moving away from the dock and all you have to use is a long rope. You know that just holding the rope by yourself won't do any good because the tanker is massive compared to you and you wouldn't have enough strength to hold it. Well you decide to wrap the rope around a strong pile that can withstand the stress of being pulled by the tanker and all of a sudden the amount of force you have to pull on the rope decreases. This may seem a little peculier because the rope is still holding the force of the tanker at bay. What is happening is friction in action.
 From: Engineering Mechanics by R. C. Hibbler
From: Engineering Mechanics by R. C. Hibbler
Above is a simplified picture of what is happening. In it we assume the rope is infact a flat belt - this will make modeling what the tensions should be a lot easier. In the picture the tensions "T1" and "T2" are two entirely differnt tensions and the reason is the belt experiences a friction force against the motion or the impeding motion of the belt. Below we will begin to explore a little of the derivation of the formula that will allow us to calculate one tension knowing what the coefficient of friction is between the belt and the stationary object is, the other tension, and the anlge β that the belt transverses around the round object.
 From: Engineering Mechanics by R. C. Hibbler
From: Engineering Mechanics by R. C. Hibbler
In the picture above we can see that the normal force acting on the belt decreases from left to right. This gives rise to varying forces of friction acting on different portions of the belt. In fact the frictional force changes at every miniscule portion of the belt as the normal force changes. This means that we need to model a differentially small element of the belt and the forces acting between it and the stationary pully. We will do this in the next picture.
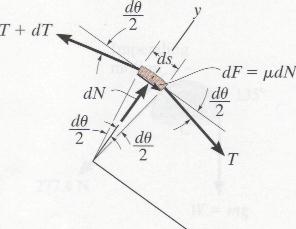 From: Engineering Mechanics by R. C. Hibbler
From: Engineering Mechanics by R. C. Hibbler
Here, what is modeled is a free-body diagram for a differentially small portion of the belt. Because html does not handle math particularly well I am including a PDF produced from LaTeX that has a derivation of the following result: If the impeding motion is in the direction of T2 then T2 = T1eμβ (see the first picture for a visual example).
PDF LINK TO DERIVATION