Analysis
So how do these laws apply to newton's cradle ?
As stated before, the physics behind Newton’s Cradle and just about any process in the universe can be extremely excessive. To simplify our task of analyzing our system, we will look at a few different scenarios of a simple motion: One ball being displaced and released. This is the simplest performance of this device, but it makes our analysis much easier. Also, the rules and laws used to predict an outcome can be used to predict the outcome of any motions of Newton’s Balls. On other thing to note is that we will be neglecting forces such as drag and friction (with the exception of a few minor comments). In reality, these play an important role in the motion, but we will only consider a “perfect system.” The motion being considered is the first demonstration in the video on the “Construction” link.
Stage 1 :
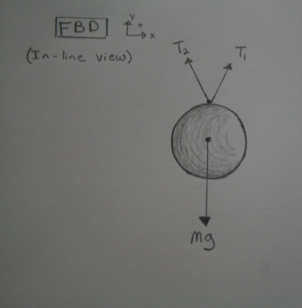
The first scenario is when the system is just sitting on a table top, and none of the balls are moving. The velocity is equal to “0” in this case, so there is no momentum or kinetic energy. Furthermore, we have set our datum for potential energy on the same axis on which the balls lie when they are at rest (as this will be the case for all scenarios). Because they indeed are at rest, the height in our energy equation is “0” and thus potential energy is “0.” Therefore both the momentum and the energy equations are: 0 = 0. Not very exciting… This does not mean that no forces are acting on the balls. Take a look at the free body diagram to the right. The force due to gravity is balanced by the vertical components of the string. The ball is in equilibrium. The horizontal components are also equal; and therefore, the ball does not move side to side. Still, not very exciting…
stage 2 :

Let’s take a look when one of the balls is displaced from its equilibrium position by an external force (human hand). Refer to the photo on the left. Again, it is a free body diagram and also a snapshot of the ball immediately after it is released. Now the forces shown are not balancing each other out, and there is acceleration. This acceleration leads to our velocity we will talk about. The vertical component of the force of gravity clearly outweighs that of the combined tensions in the strings. As the ball progresses through its path, the forces will balance to keep it on that path.
But what about our momentum and energy equations?
MOMENTUM: There is external force (gravity) acting on our body, so equations pertaining to this will not help us much. At the moment, momentum is changing.
ENERGY: Initially, there is no velocity, so initial KE is “0.” PE on the other hand is governed by (mgh)- all of which are nonzero quantities.
SUMMARY: Momentum is not yet considered. Initial energy is PE + KE, but velocity is “0” so KE is “0.” Initial PE though is simply (mgh).
But what about our momentum and energy equations?
MOMENTUM: There is external force (gravity) acting on our body, so equations pertaining to this will not help us much. At the moment, momentum is changing.
ENERGY: Initially, there is no velocity, so initial KE is “0.” PE on the other hand is governed by (mgh)- all of which are nonzero quantities.
SUMMARY: Momentum is not yet considered. Initial energy is PE + KE, but velocity is “0” so KE is “0.” Initial PE though is simply (mgh).
stage 3 :

http://stephensteach-wiki.wikispaces.com/file/view/newtons_cradle.jpg
As the balls velocity increases, the momentum and KE increase. One thing to note is that the PE is decreasing because the height (h) from our datum is decreasing while (m) and (g) are remaining constant. PE is, in a sense, being converted to KE. Now the ball is at the position it was in before anyone even touched the apparatus. It is literally at the moment of impact with the rest of the balls. This time however, the ball possesses momentum and energy; it is at its maximum velocity. These are not two different energies that the ball has at the same time. The only energy is that talked about in the energy equation. Momentum is simply a tool to predict effects of impacts, and it becomes very handy at this moment.
MOMENTUM: We want to know what will happen immediately after impact. We know that the initial momentum is going to equal the final, and the momentum is at a maximum (velocity is at a maximum). The equation tells us that the product of the mass and the velocity of the single ball is equal to the product of the mass and velocity of whatever is moving after the collision. Looking at the device, this leaves two options: when the ball strikes, the rest of the balls will move away at a much slower velocity or one ball of equal mass will move away at an equal velocity. We know that the latter is true.
ENERGY: As the ball accelerates towards the site of impact, its PE is being converted to KE. By the time the ball reaches the datum (impact site is on this), the final PE is “0” (h = 0) and the final KE is at its max. If we put these results into our equation, we find that the initial PE is equal to the final KE. By doing some measurements, we can calculate the original PE and therefore find the final KE and the velocity. This velocity is the same as the velocity for the momentum.
SUMMARY: The ball was at rest with PE stored. After the release, an imbalance of forces gave it acceleration on a curvilinear path. It gains KE while losing PE; and at the bottom of its path, it has a velocity that can be used to determine momentum. Momentum then takes over for our calculations of the next stage.
MOMENTUM: We want to know what will happen immediately after impact. We know that the initial momentum is going to equal the final, and the momentum is at a maximum (velocity is at a maximum). The equation tells us that the product of the mass and the velocity of the single ball is equal to the product of the mass and velocity of whatever is moving after the collision. Looking at the device, this leaves two options: when the ball strikes, the rest of the balls will move away at a much slower velocity or one ball of equal mass will move away at an equal velocity. We know that the latter is true.
ENERGY: As the ball accelerates towards the site of impact, its PE is being converted to KE. By the time the ball reaches the datum (impact site is on this), the final PE is “0” (h = 0) and the final KE is at its max. If we put these results into our equation, we find that the initial PE is equal to the final KE. By doing some measurements, we can calculate the original PE and therefore find the final KE and the velocity. This velocity is the same as the velocity for the momentum.
SUMMARY: The ball was at rest with PE stored. After the release, an imbalance of forces gave it acceleration on a curvilinear path. It gains KE while losing PE; and at the bottom of its path, it has a velocity that can be used to determine momentum. Momentum then takes over for our calculations of the next stage.
stage 4 :

http://di1-3.shoppingshadow.com/images/pi/25/f1/ba/46483285-149x149-0-0
On the final stage, the balls energy has dissipated into the other balls; because the balls are so rigid, a shock wave carrying the same amount of energy travels through the line of balls until reaching the last ball of equal weight. The last ball then leaves the rest and proceeds towards the apex of equal height of the initial. During this time it is decelerating to achieve a velocity of zero at the apex. Although the energy is not needed and not considered for calculations while energy is being transported through the balls, it “reappears” in our calculations when the last ball goes into motion. Momentum will tell us what we need to know about that last ball right when it leaves; but anytime after that, an imbalanced force, gravity, is acting on it. To follow what’s going on till the apex, we use the conservation of energy.
MOMENTUM: We’ve just had a collision here. By using energy, we found our velocity and, in turn, our momentum. In order to conserve this, we need to have a balanced reaction. Very simple put, the first ball throws all of its momentum into the line of balls. Because the balls are not all attached, the momentum travels to an object of equal mass (the last ball) and gives it an equal velocity. This is predicted by the equation, and the velocity of another different sized ball could be calculated using the same equation. This is the only collision we will look at (even though this will repeat several times), so momentum is done for our purposes.
ENERGY: As stated before, the energy is still present, but not needed in our analysis of the shock wave. It takes back control of our system as soon as the last ball leaves the chain, though. Simply put, the energy takes the reverse path of the starting ball. KE begins to be converted back to PE until the velocity equals “0” and the height is the same as the starting ball.
SUMMARY: The ball slams into the balls at rest. Energy is transferred from one to the next until the momentum of the first ball equals the mass and then instantly the velocity of another- the last ball. This ball decelerates to the apex while losing momentum and KE. Eventually, the PE at the apex is equal to that of the original PE.
MOMENTUM: We’ve just had a collision here. By using energy, we found our velocity and, in turn, our momentum. In order to conserve this, we need to have a balanced reaction. Very simple put, the first ball throws all of its momentum into the line of balls. Because the balls are not all attached, the momentum travels to an object of equal mass (the last ball) and gives it an equal velocity. This is predicted by the equation, and the velocity of another different sized ball could be calculated using the same equation. This is the only collision we will look at (even though this will repeat several times), so momentum is done for our purposes.
ENERGY: As stated before, the energy is still present, but not needed in our analysis of the shock wave. It takes back control of our system as soon as the last ball leaves the chain, though. Simply put, the energy takes the reverse path of the starting ball. KE begins to be converted back to PE until the velocity equals “0” and the height is the same as the starting ball.
SUMMARY: The ball slams into the balls at rest. Energy is transferred from one to the next until the momentum of the first ball equals the mass and then instantly the velocity of another- the last ball. This ball decelerates to the apex while losing momentum and KE. Eventually, the PE at the apex is equal to that of the original PE.
summary
In a perfect system, the scenarios and results discussed would be valid. However, considering drag, friction, energy lost due to thermal energy, etc., these results aren’t going to happen. This explains why Newton’s Cradle does not continually cycle on into eternity. Newton’s Cradle is still an excellent example of the conservation of both momentum and energy. Both of these laws still hold, but the surroundings add extra components that need to be considered. This site offers a very simplistic and hypothetical scenario to explore these laws. Newton’s Cradle is more than a fancy table decoration; it represents the ideas and thoughts of one of sciences most renowned thinkers. But more importantly, it sheds some light on the some mysteries that govern our universe…