Back Next
Introduction
The purpose of learning Fireground Hydraulics is to quickly calculate the correct pressure a pump must be set at in order to provide the correct nozzle pressure for a variety of firefighting operations. Whether supplying another engine, master streams, or the handline carried in by an interior attack crew, firefighters need to have sufficient gallons per minute (GPM) of water flow to combat the heat and energy of a fire. It comes down to the engine driver/operator to provide water, which often means calculating pressures rapidly, even in the face of emergency.
While all fireground hydraulics are based off of complicated equations often used to describe the physics of the real world, such equations are not always simple to solve when things get down and dirty. Imagine trying to solve Bernoulli's Equation,
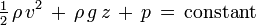, (rho=density of water,
v=velocity of water, g=acceleration
due to gravity, z=height, p=pressure) in a split second. Seems
like a daunting task, right? Add in the pressure of a structure
fully engulfed in flames, knowing that it is up to you to provide the
right amount of water to extinguish the inferno. Just the thought
of doing math at a time like this is enough to stress even the veteran
fire engineer. Thanks to a little knowledge of fluid physics and
mathematical simplification however, the situation descibed above
becomes much easier to handle. That's where fireground hydraulics
come in. Though not as accurate as the calculations that went
into the creation of virtually all fire apparatus and appliances
(equipment that water flows through), the equations
presented on following slides are just as effective in speeding fire
extinguishment. 