Attraction
between Planet and Meteoroid:

Impression of a Meteoroid
approaching Earth
Photo from TIME Magazine
(Denis Scott / Corbis)
So now we know where
the asteroids come from, but how do they
move
towards a planet as they do?
Mostly, it's Newton's Law of
Universal Gravitation at work.
Basically, it says that every
thing has an attraction to another object
because of gravitational force.
This gravitational force is
defined by: F=GMm/r2
.
The M and m are the two different masses in
question while r is the radius
(distance)
between them.
G is the gravitational
constant, which is: G=6.667X10-11
Nm2/kg2.
This means that the attraction
between any two objects greatly
increases when the masses are large and when the distance between them
is small.
Note that the gravitational
constant is small, and so it isn't seen as
well on a smaller scale.
So as a meteor comes closer to
a planet, the pull between them greatly
increases.
Like planets, asteroids move
in orbits that are similar to the orbits
of planets around the sun.
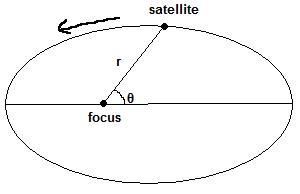
Rough Diagram by Me.
They follow Kepler's
Laws, which are:
- All planets move in
an elliptical orbit around the focus.
Note that the focus is not necessarily
at the center.
- A hypothetical line
joining the satellite and the focus sweeps
out equal areas in equal time intervals.
In other words, the closer to the focus
the
object is, the faster it travels.
- The square of the
planet's period is directly proportional to the cubed semimajor axes.
The period (T) is the time the satellite takes
to complete the ellipse.
Kepler's 3rd Law comes out as: T2=(4pi2/GM)r3.
M is the mass of the focus object.
There are things that can
knock asteroids out of their orbit, however,
such as an impact with another
asteroid, going near a magnetic field, or gravitational force.
These are the sorts of things
that send asteroids towards another space object, such as Earth.
<--From
Asteroids and Comets
Home
In the
Atmosphere -->


