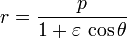
Kepler’s Laws

Johannes Kepler was a German mathematician and astronomer. He monitered the movements of the planets and worked with the observations of fellow contemporaries like Tycho Brahe. Through intensive research, Kepler would develop what would become known as Kepler’s three laws of planetary motion.

1.       The orbit of every planet in the solar system is an ellipse with the Sun as the focus.

2.       A line joining a planet and the Sun sweeps out equal areas during equal time intervals.

3.       The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.

              The above laws are still used in modern times to approximate the orbits for artificial satellites. They are useful only when a relatively small body orbits about that of one with a much larger mass. The mathematical representations of the his three laws are presented below.

Kepler’s First Law:

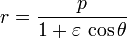
r=\frac{p}{1+\varepsilon\, \cos\theta}

                R (r) and theda represent the polar coordinates of the given planet or satellite. P (p) is the semi-latus rectum, or half the chord perpendicular to the directrix and passing through the focus. E is simply the eccentricity of the elliptical orbit.

Kepler’s Second Law:

\frac{d}{dt}\left(\frac{1}{2}r^2 \dot\theta\right) = 0,

                In this equation 1/2r^20 represents the areal velocity, or the rate at which area is created (or pronounced) as a given orbiting body moves along its path.

Kepler’s Third Law:

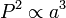
{P^2} \propto {a^3}

                Here, P represents the orbital period of the orbiting body and a is the semimajor axis of the given orbit.

Last    Next