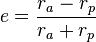
Orbital Elements
Orbits can vary greatly in size and shape. Such variations exist that it takes the culmination of six identifying features to describe one independently. These parameters are often referred to as orbital elements, and include inclination, longitude of the ascending node, argument of periapsis, eccentricity, seminmajor axis, and mean anomaly at epoch.
1. The eccentricity of an orbit is what defines its absolute shape. An orbits eccentricity will define whether or not an orbit is circular, elliptical, parabolic, or hyperbolic and to what extent it is of each. Eccentricity is zero for circular orbits, and, for elliptical orbits, is defined by the equation below,
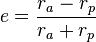
where ra is the radius of the apoapsis (the farthest distance of the orbit from the center of mass) and rp is the radius of the periapsis (the closest distance to the center of mass).
2. The semimajor axis is defined as the “distance between the geometric center of the orbital ellipse with the periapsis (point of closest approach to the central body), passing through the focal point where the center of mass resides.”
3. Inclination refers to the angle at which the orbital plane is tilted with respect to a particular plane of reference. With orbits, the inclination is often taken with respect to that of the Earth’s equator.
4. The longitude of the ascending node refers to the “ascending node of the ellipse (where the orbit passes upward through the reference point) with respect to the reference frame’s vernal point.”
5. The argument of periapsis refers to the orientation of the ellipse within the orbital plane.
6. The mean anomaly of the epoch is defined as the location of the satellite in orbit along the orbital ellipse at the epoch.