Now that we have an idea of how gases behave and of what entropy measures, we move onward.
We now introduce a formula for entropy that was derived from the statistical approach.
This formula is: S=Nkln(V) where N is the number of molecules of gas, k is a special constant, and V is the volume taken up by the gas.
Somebody sat down, thought about it a while, and then said, well, wouldn’t the entropy change if we modified the volume. According to the above formula it would. Say we doubled the volume by pulling out a partition between the segments:
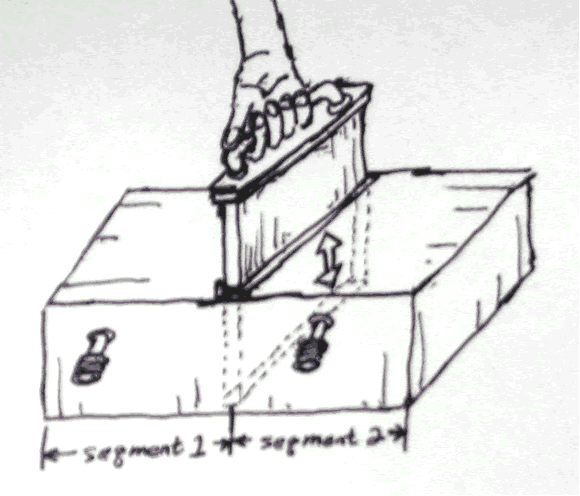
Initially for segment 1 we had: S1=(V1), Initially for segment 2 we had: S2=(V2)
We assume that each segment has 1 mole of gas. This makes 2 moles of gas in the entire configuration.
We assume each segment initially has 4m3.
We can calculate the initial entropy in each of these segments:
S1intial=S2initial=N2*k*lnV2=6.02*1023*ln4=8.345*1023
After the partition is removed we get: Sfinal=N1+N2klnV1)+N1+N2k(lnV2= N1+N2*k*lnV1+V2=2*6.02*1023*ln8=25.036* 1023
∆S = 25.036* 1023- 28.345*1023=8.346*1023. Here the entropy has increased. You multiply be two to account for the entropy of each side (segments 1 and 2) before the partition is removed.
Obviously the entropy changed. However, here’s the thing, if you have the same gas in both sides before the partition is removed, a heat and temperature change isn’t recordable. Some people have even said the temperature will decrease. Let’s see an example of decreasing entropy:
Now we put the partition back in place and then add another partition into one of the segments (segment 1).
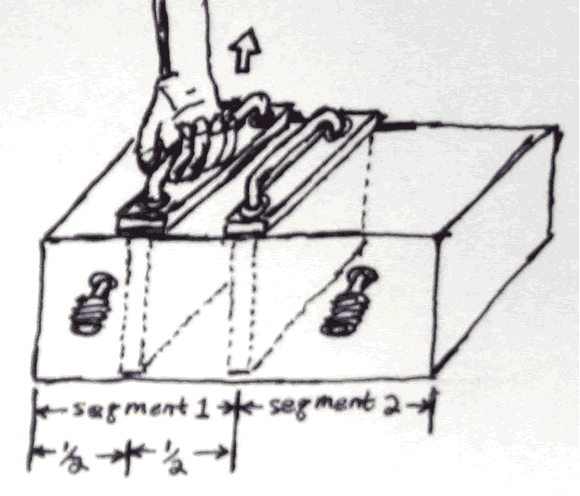
Before the partition is inserted we have in segment 1: S1intial=N1*k*lnV1=6.02*1023*ln4=8.345*1023
After the partition is inserted we have: Sfinal =N2lnVfinal=N2klnV2= N2kln2m3 for each of the segments.
S final=2*6.02*10232*ln2=6.02*1023*ln2= 4.1727*1023= N2ln4
The entropy change is then:
S final – S initial = 4.1727*1023- 8.345*1023= -4.1727*1023
The entropy here has decreased by adding a partition.
A popular way to write the formula is: ∆S=Nklog(V2V1). This confuses people because it assumes the number of moles doesn’t change, but the volume does. I don’t use this, because the moles change when partitions are added or taken away in direct proportion to the volume!
In the calculations I’m ignoring K and I’m also ignoring part of the formula.
The original formula varies from site to site. Hardly any two sites had the same formula. I only found two sites that had the same formula out of six different sites.
This formula was: S = Nk(lnV) + 1.5NklnT + σ
I deleted the second and third parts. σ was said to be a constant. I’m also assuming the temperature T was constant. Okay, so if the temperature did change a lot, would that compensate and make the entropy change zero. Obviously the amount of gas enclosed per given volume doesn’t change any, so why would the temperature change in the first place?
These sites are:
Http://www.nyu.edu/classes/tuckerman/stat.mech/lectures/lecture_6/node5.html
http://home.fnal.gov/~neilsen/publications/demon/node6.html
Another website: http://bayes.wustl.edu/etj/articles/gibbs.paradox.pdf
uses the following formula:
∆S=NklogV2V1+32NklogT2T1
I got this from chapter 7. The Pauli Analysis, under equation 8.
This website uses the same formula but has base ten logarithms instead of natural logarithms.
I will rewrite this formula as: ∆S= NklogVfinalVinitial=NklogVfinal-Nklog(Vinitial)
Again, I’m ignoring the temperature term and I vary the N in proportion to volume. The above formula is for a change in volume by adding a partition without the moles changing. It would originally be: S final= NklogVfinal-Nklog(Vinitial). A better way to think of it would be like a piston compressing a substance where the heat term would be incorporated. Thermo Muzzie isn’t going to be inserting a partition here to divide the moles.
We have the same units as earlier. We have 1 mole, and 4 m3 for each of the original two segments.
Inserting a partition in segment 1 gives: S final=2*N*k*log(2m3)=2*6.02*〖10〗^232*log(2)= =1.81*1023. Notice we multiplied by 2 because you have two segments and you need the entropy of each to have the same final and initial volume in the measurement.
The original entropy of segment one before it was divided is: S initial=Nklog4m3=1*6.02*1023*log4=3.624*1023.
∆S =Sfinal-Sinitial=1.81*1023-3.624*1023=-1.81*1023
Oh no, we got negative entropy again. If you make the segment 1 initial volume 8 m3 then the final volume after Inserting a partition in segment 1 gives: S final=2*N*k*log(4m3)=2*(0.5*6.02*1023)*log(4)=3.62*1023.
The original entropy of segment one before it was divided is: S initial=Nklog8m3=1*6.02*1023*k*log8=5.43*1023
∆S =Sfinal-Sinitial= 3.62*1023-5.43*1023=-1.81 * 1023
Therefore, we can establish that the entropy change doesn’t depend on the volume which makes it even more confusing. So it would go all the way down to the atomic scale. Let’s double check by trying 20,127 m3 as the original volume to make sure this isn’t a trick.
The final volume after inserting a partition in segment 1 gives: S final=2*N*k*log(10,063.5m3)=2*(0.5*6.02*1023)*log(10,063.5m3)=24.09 * 1023
The original entropy of segment one before it was divided is: S initial=Nklog20,127m3=1*6.02*1023*k*log20,127=25.908*1023
∆S =Sfinal-Sinitial= 24.09 * 1023-25.908*1023=-1.818 * 1023
This means that entropy can go all the way down to the atomic level. However, this is only theoretical, and assuming you don’t vary the moles. This is where Joseph Von Neumann headed as well as many other people, and that’s where I can’t follow what’s going on because the math gets crazy as well as the theories.
For a final example we take away a partition using base ten:
We assume like before that each segment has 1 mole of gas. This makes 2 moles of gas in the entire configuration.
We can calculate the initial entropy in each of these segments:
S1intial=S2initial=N2*k*logV2=6.02*1023*log(4)=3.62*1023
After the partition is removed we get: Sfinal=N1+N2klnV1)+N1+N2k(lnV2= N1+N2*k*lnV1+V2=2*6.02*1023*log(8)=10.87* 1023
∆S = 10.87* 1023 -2( 3.62) * 1023= 3.63*1023. Thus the entropy change here is positive and is one third of the initial entropy just like with base e.
So why does the entropy increase according to math in some cases and decrease in others? Does it depend entirely on different gases, or can the same gas be used? Is it a quantum effect? Is it due to the Gibbs particle? Is it what causes time to vary?
Here’s the paradox, and lots of more mathematically gifted people than myself have spent hours working on this paradox to see what is going on. A popular way to fix the paradox has been to use a quantum approach with an equation called the Sackur-Tetrode Equation. One gifted mathematician, Joseph Von Neumann, came up with his own quantum theory that the entropy decreased in certain cases of adding partitions. Since this guy was so gifted, and since entropy isn’t supposed to decrease, this caused a lot of people to study the topic. The best answer most people give is that the math is flawed, and then they go into the realm of quantum mechanics to explain why this is true. On the next page are some ideas for further experiment.

