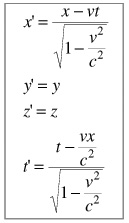Lorentz Transformation Equations

Lorentz Transformation Equations

In the introduction I mentioned that classical mechanics required the use of Galilean Transformation equations to transform the results in one inertial frame of reference into another inertial frame. However, as was already shown, this transformation becomes less and less accurate as the velocity of the body approaches the speed of light. Therefore, we need another way to determine how to transform the information into another reference frame.

http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/ltrans.html#c2

Before Einstein created the Special Theory of Relativity, Henkrik A. Lorentz created the Lorentz transformation equations for studying electromagnetic phenomena. However, Einstein soon realized that these same equations could be used to explain physics phenomena as well and promptly included them with the theory. The equations for transforming into a moving frame of reference (x prime, y prime, z prime, and t prime coordinates) are on the left. Note that only the x prime and t prime frames are affected. This is a very important result because it says that relativistic effects, length contraction in particular, only affect the object in the direction of motion. In other words, if an object were traveling strictly along the x axis, length would be contracted in the x direction only. The y and z directions would be unaffected by the velocity of the object.

http://appletree.mta.ca/courses/physics/4701/EText/LorentzTransformation.html

To further explain these equations, let's set up a hypothetical situation. Let's say we have a system like the one on the right. A stationary observer in the S frame observes an event in the S prime frame. The S prime frame is moving with a velocity v relative to the S frame. Therefore if we had the coordinates of an event in the S frame, we could find out the corresponding coordinates in the S prime frame. The y and z coordinates would translate directly to the other frame, but the time on the axis on which the S prime frame is moving would need be transformed. All that would need to be done is to plug in the S frame x coordinate and the velocity of the S prime frame with the time into the first equation to get the x prime coordinate, and the same to find the time in the S prime frame. To find the coordinates in the S of an event in the S prime frame, simply replace the primed terms with the unprimed terms and vise versa.