Physics Behind Pitching

picture provided by Google
The
physics of pitching entails
that one uses a barrage of techniques to hurl a baseball towards home
plate and
cause the batter to not hit it. A throw
is different than typical standard projectile due to rotational force
that is
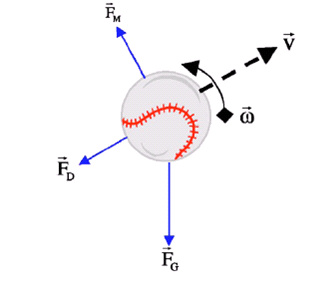
applied to the baseball. The forces
which act on the ball are the drag force, the normal force, the force
of
gravity on the ball, the initial force applied to the ball causing it’s
initial
acceleration. However, it also was
angular velocity which in turn exerts a force on the ball altering its
flight
path (a sample diagram of the forces in action are pictured to the
left). Furthermore, in order to calculate
the drag,
gravity and normal forces which in turn all have an effect on the
ball’s
trajectory can be calculated by the formula to the left.
The flight plan of the ball is made even more
interesting by the “Magnus Force” to which is created by high angular
rotation
of a ball.
The
Curve Ball and How it Works
 This
“Magnus Force” to which I referred to in the previous slide is as a
direct
result of the pitcher throwing the ball so that the axis of rotation in
relation to the ball is not perpendicular to the ground.
As a result of this altered axis the Magnus
force of the ball will ultimately curve left or right.
An example of this is pictured at right. This
is based on the
This
“Magnus Force” to which I referred to in the previous slide is as a
direct
result of the pitcher throwing the ball so that the axis of rotation in
relation to the ball is not perpendicular to the ground.
As a result of this altered axis the Magnus
force of the ball will ultimately curve left or right.
An example of this is pictured at right. This
is based on the 
where
A
is
the cross sectional area of
the ball, v
is
its speed,
_
is
the air density _1.23
kg/m3_,
and CD
and
CL
are
the drag
and
lift coefficients, respectively.15We
will
focus only on CL.
Data
on other spherical sports balls suggest that CL
is
mainly
a
function of the spin factor S=R_/v,

When a
pitcher
throws a
curve ball, he will throw it such that the axis of rotation is not
perpendicular
to the ground, as it is in a fastball.
Because it is
spinning in a skewed axis,
the Magnus force will force the ball to curve in a horizontal direction
instead
of vertical "curve" of a fastball.
How much will
a baseball
curve?.
The equation is as follows (from Prof. Adair's book Physics of
Baseball):
Magnuson Force = KwVCv
where:
- FMagnus Force is
the Magnus Force
- K is the Magnus Coefficient
- w is the spin frequency
measured in rpm
- V is the velocity of the
ball in mph
- Cv is the drag
coefficient
http://library.thinkquest.org/11902/physics/curve2.html

http://www.thecompletepitcher.com/pitching_grips.htm#q7