Home   The Field   Pitching   Catching  Bibliography
Physics of Hitting

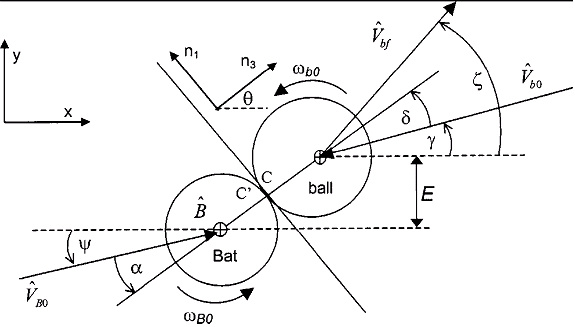                                           The most basic concept of hitting is to put the bat on the ball.  Similarly, this basic concept is also a utilization one of the most basic theories of physics, Newton’s third law of physics “for every action there is an equal and opposite reaction.”  By the hitting the ball it puts “the ball in play.”  However, if one wanted to learn how to hit a home run the individual would want to use enough force to hit the ball over the fence for a home run, and then at the same time to hit the ball causing it to fly at an angle 45 degrees to the field, this would in turn result in the maximum distance to be achieved.  In order to calculate the angle of trajectory of the ball after it is hit, you can use the formula as outlined by the diagram to the right.  The diagram shows all forces involved in calculating the trajectory.  This is done by factoring in all forces (wind resistance, loss of energy to sound, velocities, etc.)  and in doing so ensuring that the net energy and momentum is conserved from     the initial to the final reaction.  The hitting aspect of baseball through calculations and worldly physics allow us to explain all reactions between objects and people    that occur throughout the course of the game, including the physics of pitching as well.

 

                                     

                        Symbol Description Value

G - Gravitational acceleration constant 9.81 m/s2

m - Static coefficient of friction - 0.5060.04 wood/ 0.3560.03 aluminum

n - Kinematic viscosity of air - 1.5e25 m2/s

CD -  Drag coefficient

CL  - Lift coefficient

Mb -  Baseball mass - 0.145 kg ~5.1 oz!

MB 8 - Bat mass  - 0.9 kg ~31.7 oz!

rb  - Baseball radius - 0.0366 m ~1.44 in.!

rB  - Bat barrel radius - 0.0350 m ~1.38 in.!

kB1  - Radius of gyration of bat for c.m. about n1 axis - 0.217 m ~8.54 in.!

kB2  - Radius of gyration of bat about n2 axis - 0.0231 m ~0.91 in.!

kb  - Radius of gyration of ball about c.m. - 0.0247 m ~0.97 in.!

E - Undercut distance

u - Angle of common normal n3 from horizontal

a - Bat swing angle from common normal

b - Bat swing angle from horizontal

g - Pitched ball velocity angle from horizontal

d - Pitched ball velocity angle from common normal                                                                                                                                                               Pic taken by K. Lauritzen  (2005)

V ˆ

b0 -  Pitched ball speed at plate

V ˆ                                                                                                                                                                                                                                                

B0 -  Pre-impact bat speed at B ˆ                                                                                                                                                                                    

vb0  - Pre-impact ball spin magnitude

vB0  -  Pre-impact bat spin magnitude

vb f   -  Post-impact ball angular velocity

Vw -  Wind velocity

V ˆ

b f  -  Post-impact ball c.m. velocity

Vb f   -  Post-impact ball velocity at contact point

VBf  -   Post-impact bat velocity at contact point

z   -  Post-impact ball velocity angle from horizontal

                                            1154 Am. J. Phys., Vol. 71, No. 11, November 2003 Sawicki, Hubbard, and Stronge 1154