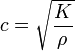Speed of Sound in Water

A sound wave propogating through water consists of alternating compressions and refractions of the water. Theses compressions and refractions are picked up by a receiver and on the sound veloctiy probe. The speed changes based on the water temperature, depth, and salinity. For most applications of sonar, the speed of sound can be taken to be about 1500 m/s^2 on average. However, for sound moving through seawater, the speed can range from 1440 m/s to 1570 m/s.

The speed of sound through water depends mainly on three variables. The temperature of the water, the salinity, and the pressure. Earlier, we stated the speed of sound, c, through an elastic medium is

In order to account for the variance due to the change in temperature (a change of 1 °C ~ 4 m/s), salinity (a change of 1‰ ~ 1 m/s), and pressure (and therefore depth), we need different equations.

An empirical equation for these variables has been derived and is reasonabley arccurate. This equation was derived by Mackenzie and presented in his article "Discussion of sea-water sound-speed determinations". The equation is:

c(T, S, z) = a1 + a2T + a3T2 + a4T3 + a5(S - 35) + a6z + a7z2 + a8T(S - 35) + a9Tz3

where T, S, and z are temperature in degrees Celsius, salinity in parts per thousand and depth in meters, respectively. The constants a1, a2, ..., a9 are:

a1 = 1448.96, a2 = 4.591, a3 = -5.304×10-2, a4 = 2.374×10-4, a5 = 1.340, a6 = 1.630×10-2, a7 = 1.675×10-7, a8 = -1.025×10-2, a9 = -7.139×10-13

with check value 1550.744 m/s for T=25 °C, S=35 parts per thousand, z=1000 m. This equation has a standard error of 0.070 m/s for salinity between 25 and 40 ppt. A sound speed calculator can be found at http://resource.npl.co.uk/acoustics/techguides/soundseawater/.