|
The action of turning requires the same physics
required for balancing while adding another layer of
difficulty in order to rotate. When executing a
turn, a dancer must exert a frictional horizontally
against the floor where a frictional force will
oppose it. This force is perpendicular to the radius
of the rotation, therefore it produces a torque on
the dancer's body which initiates rotation. There
are different starting points for turns that differ
in difficulty. One of the easiest ways to begin a
turn is to start in what is called fourth position
(demonstrated on the left side of the top figure).
The reason this is easier is because, since there is
a larger distance between the feet, the force
applied creates a larger torque given that torque is
the product of the force applied and the distance
from where it is applied to the center of the turn.
The right side of the top figure is illustrating
that turning from one foot is much more difficult
because the distance between the two forces is very
small, leading to a smaller torque. The position of the body while it is turning contributes to the speed of the turn. A dancer's rotational inertia is determined by their mass and its distribution. If the mass is located further away from the center of the turn, then the rotational inertia becomes larger. The laws of physics state that momentum is always conserved, and rotational momentum is the product of the objects rotational inertia (I) and its rotational velocity (  );
therefore, if rotational inertia is increased,
rotational velocity must decrease. In short it can
be determined that if a dancer distributes their
mass further away from their center they will spin
slower (larger rotational inertia=smaller rotational
velocity) and vice versa. |
 Laws, K. (2002). 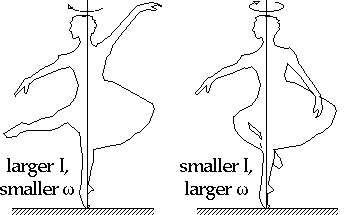 http://www.hep.uiuc.edu/home/g-gollin/dance/dance_physics.html#5 |
http://balletclassroom.wordpress.com/2012/03/22/361/
