Core Terminology and Concepts

Generalized Coordinates:
 In Lagrangian Mechanics, instead of using a traditional coordinate system, one is free to employ whatever coordinate system is most convenient for solving a particular problem. These generalized coordinates are often denoted q1,q2,q3,...qn.They are commonly are spherical or cylindrical coordinate systems, which are generally cumbersome to work with using Newton’s formalism. The time derivatives of generalized coordinates are called generalized velocities, written here as


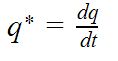
q*=dq/dt

Constraint Equations: In  some systems, the possible motion of objects is constrained to a particular path or set of possible paths. These can be written in equation format, and the number of these equations is subtracted from the system’s total number of degrees of freedom.
Degrees of Freedom:
A degree of freedom is simply a way that a system can move, by translation or rotation. In three dimensions, the number of degrees of freedom a system has is 6n-m. Where m is the number of constraints on the systems
motion, and n is the number of objects. Those six degrees of freedom correspond to translation in the three dimensions of space and rotation about three mutually perpendicular axes. If a system consisting of one object is restricted from rotation, three equations of constraint are introduced (one for each axis of rotation) and the number of degrees of freedom of the system 6(1)-3=3, corresponding to unrestricted translation.

Generalized Forces:
When non-conservative forces act on a system, those forces can be related to generalized forces (a term in the Euler-Lagrange equation) by multiplying the applied force by the instantaneous rate of change of the object’s position with respect to a generalized coordinate. A generalized force is usually written as Q, where

Introduction - Principle of Least Action - Euler-Lagrange Equation - Example of Lagrangian Mechanics


Bibliography