Critical Angle
Looking at the Snellís Law we
can find a few interesting properties of how light interacts
with materials. In the case of light hitting the surface at
a perfectly perpendicular angle, then sin would have to be
sin0, which is just zero. Having one term of the equation be
zero, zeros out the rest of the equation. This means that
there is no change in the angle of refraction no matter what
the Refractive Indexes of the media. We can also see that if
Refractive Indexes of the two materials are the same, there
would be no change in refracted angle.

From: The Physics Classroom
Perhaps more interestingly,
we can also predict a strange phenomenon of light, Total
internal reflection. Manipulating the equation, we can
arrive at the following form:
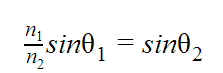
Now imagine a case of light
leaving a very dense material and entering a much less
dense material. This means the change of angle of light
between the media will be very large. Now imagine that the
light is also entering at a very large angle, that is,
very far off from the normal. This could force the
refracted angle to be more than 90 degrees, meaning the
light would never actually leave the first material, and
would be reflected back. Now, this may seem like itís a
problem with bounding the equation, but it really does
hold up in the real world. This is a concept that both
explains natural phenomena and is exploited in technology.

From: Wikimedia Foundation