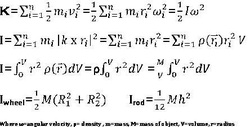The Physics of a Water Wheel
Newton's Laws for Rotation
- If an object does not experience a net torque on it, it will not have an angular acceleration and therefore no angular velocity. If there is a net torque on an object it will have an angular acceleration and angular velocity.
- The torque on an object is equal to the moment of inertia multiplied by the angular acceleration.
Moment of Inertia Formulas
The Moment of Inertia
The moment of inertia of an object is also referred to as the rotational inertia and is basically the rotational mass of an object. In order to determine this we need to look at an objects rotational Kinetic energy. Kinetic energy is one half the objects mass times its linear velocity squared, but when an object like a water wheel is traveling in circular motion the rotational Kinetic energy has to be considered. Now considering the rotational Kinetic energy it is defined by one half the first derivative of time with respect to angular displacement(angular speed) squared multiplied by the radius squared times the mass of the object. In the case of a water wheel we have a thick hollow cylinder(wheel) and a rod(axle). The inertia is defined as the sum of the points of mass multiplied by the corresponding radius squared. In order to find the Moment of Inertia for an individual object we need to look at it as a collection of equally sized masses, which means that they have equal densities and volumes, so if we integrate the perpendicular distance(radius) squared from the center of mass multiplied by the mass density and integrate it with respect to the volume of a particular object we can calculate the moment of inertia of an object.
Torque
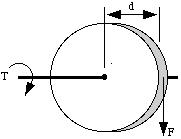
Torque or the moment arm is quantified by taking the cross product of the force perpendicular to the axis of rotation and the position vector, taking the dot product of these gives us the SI units of Nm. To get the magnitude of torque it is also important to take into consideration the angle theta between the force vector and the position vector. Use the right hand rule to determine the direction of torque for the given position vector and force.
solarbotics.net
Torque Formulas
Work Formulas
Rotational Work
The Work done by torque is defined as the torque multiplied by the angular displacement.
In order to determine how much work can be done by moving water in a river or stream requires that the total volume of water available to do work is determined. Once a volume is determined, it is possible to calculate the amount of work that the water is capable of doing on the water wheel and in turn the ideal size and type of wheel can be determined.