 VOLUME AND SOUND
INTENSITY:
VOLUME AND SOUND
INTENSITY: 
How loud IS cranking it up to 11?
Sound intensity is defined as the power per unit area, which in the case of sound, is the Watt per square meter (W/m2). This means that the spherical motion of the sound causes its intensity to vary with distance from the sound's source.
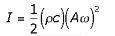 |
| http://www.insula.com.au/physics/1279/L14.html |
where
ρ is the density
of air,
ω is
the frequency of the wave (discussed more on the frequency page),
C is
the
speed
of
the
wave,
and
A is the amplitude of the wave, depending on the radius (that is,
distance from the source).
 |
As a result of this
equation, we see that as the distance from the source of the sound
increases by a factor of some number N, the intensity of the sound is decreased by a factor of N2.
The opposite, however is also true. If the distance is decreased by some factor N, then the intensity of the sound is increased by N2. So if you are standing 10m from a loudspeaker at a concert, and you move to 5m away, the intensity of the sound coming from the speaker is now 4 times what it had been at 10m. This is important to keep in mind so as not to damage your hearing the next time you attend your favorite band's show. |
| Photo courtesy of
http://hyperphysics.phy-astr.gsu.edu/hbase/ph4060/p406i.html |
Note: the equation for the
intensity of sound in this diagram comes from the power written as a
fraction of the sphere's area. This is another approach to sound
intensity. |
Volume is simply a scale of sound intensities.
One way to describe volumes is on a logarithmic scale, using what is
known as the Bel.
The Bel was named
for Alexander Graham Bell, who is credited in the West as inventing the
telephone. However, more commonly used is the decibel, which is simply
a scale in units of one-tenth of a Bel. This system was derived solely
to describe the types of sounds that the human ear was capable of
hearing. The scale is logarithmic because the sounds that a human ear
can process vary greatly over a wide range of sounds.
The
equation
for
the
decibel
is represented as follows:
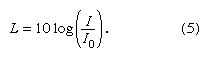 |
| http://www.britannica.com/EBchecked/topic/555255/sound/63970/The-decibel-scale |
Where L is the sound level,
I is the intensity of the object's sound, and
Io is a fixed value of 10-12 W/m2,
which is the minimum intensity that the human ear can hear.
Here are some examples of common sounds and
their decibel levels:
| Quietest sound heard |
0 dB |
| Background sound in a library |
30 dB |
| Golf course |
40-50 dB |
| Street traffic |
60-70 dB |
| Train at railroad crossing |
90 dB |
| Dance club |
110 dB |
| Jack hammer |
120 dB |
| Jet taking off from an aircraft
carrier |
130-150 dB |
Additionally, since the sound level is dependent upon sound intensity, and intensity is dependent upon distance from a sound's power source, it is also worth noting that the sound level also decreases when the distance from the power source increases. So it is possible to lower the sound level of an object simply by moving farther away from it.