The Downhill Mechanics of Sledding
There are a lot of forces that act upon a sledder as
they travel down a hill. The forces involved in sledding are gravity, friction,
and the normal force. Another force is air resistance, but for the sake
of simplifying things we will ignore it. Gravity is what allows you
to slide down a hill. On the other hand, friction is a force that works against
you, causing you to slow down.
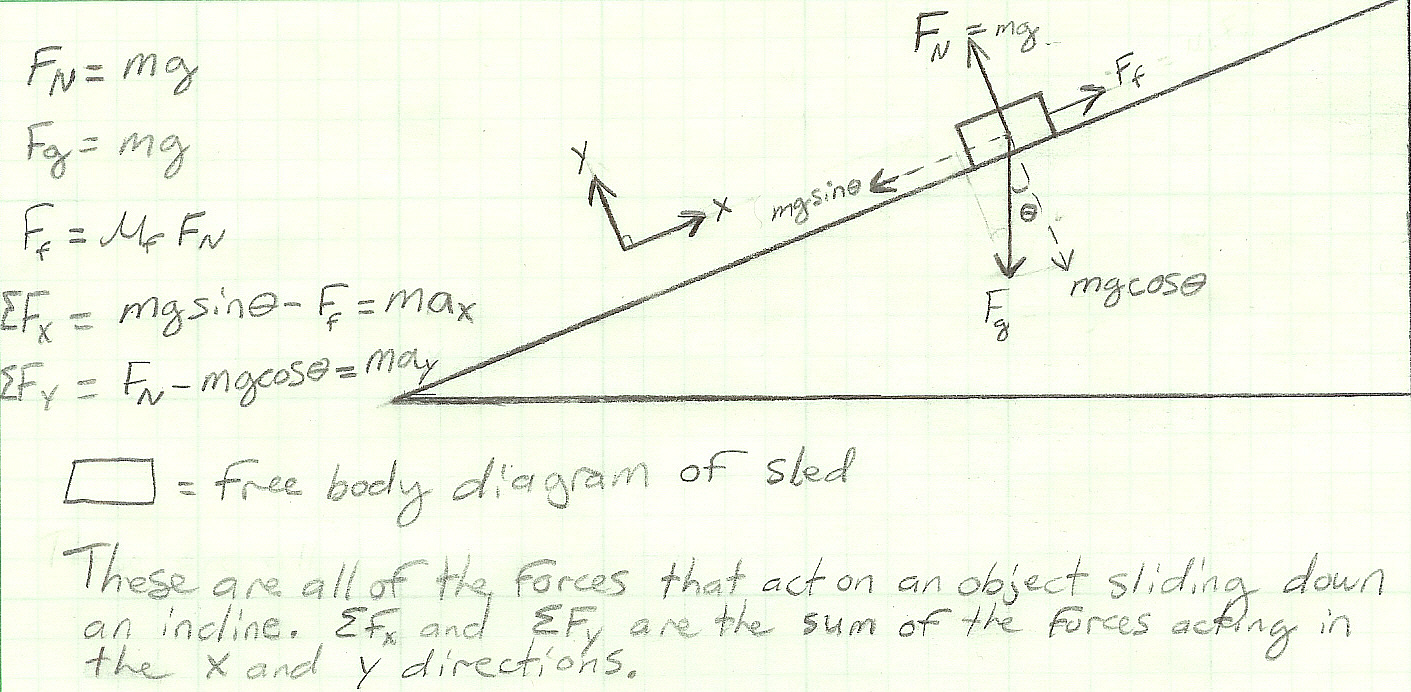
But first, a few words about force. Force is mass times acceleration (F=ma) which is Newton's second law. Where it says that the acceleration of a body is proportional to the net force acting on the body and is inversely proportional to its mass (physics notes from class). Force is a vector because it has direction and magnitude. The units for force are Newton's (kgm/s²).
Drawn by Ryan Boothe
But first, a few words about force. Force is mass times acceleration (F=ma) which is Newton's second law. Where it says that the acceleration of a body is proportional to the net force acting on the body and is inversely proportional to its mass (physics notes from class). Force is a vector because it has direction and magnitude. The units for force are Newton's (kgm/s²).

Drawn by Ryan Boothe
The force of gravity pulls in the downward direction, which
is what pulls the sled down the hill. Gravity is the acceleration of objects
to the center of the earth and its value is 9.81m/s². The normal force
prevents objects from falling and is "the component of the weight normal
to the plane...this is the normal force" (Feynman 12-4). Say, for example,
you have a mocha sitting on your desk to help you study late into the night
for an exam. Well, the force that is keeping that mocha from falling to
the floor is your desk. This upward force from the point of contact between
the mocha and the desk is the normal force. The force of gravity pulls
down towards the center of the earth while the normal force is the force
from and object that is exerted on the mocha to keep it from falling towards
the earth. There are no forces in the horizontal direction causing the mocha
to move, so the net force of the horizontal direction is zero. The same
is true for the vertical direction; the mocha on the desk is not moving up
or down. The normal and gravitational forces acting on the mocha on the desk
cancel each other since the mocha is not moving, so the net forces in the
vertical direction equal zero.
Back to the sled. Another force that acts on the sled is friction. There are two types of friction, static and kinetic friction. Static friction is the resistive force that prevents an object from moving from a stationary position. The other type is kinetic friction which occurs when one object slides on another object (Feynman 12-4). The general equation for finding the force excerpted by the static and frictional force is F=µN. The µ symbol is the coefficient of friction which varies between 0 and 1. There is a subscript of either an f or s for µ when finding one or the other. (N) stands for the normal force which equals the mass in kilograms times the acceleration of gravity, 9.81m/s². Frictional force is a non conservative force and does work on a system. Friction causes a change in the mechanical energy of a system into internal energy and therefore is not conservative (Serway and Jewett pg. 229).
So, this means that, when you sled down a hill, there is a resistive force that works against you making you slow down and causes you to stop and the bottom of the hill. Work is being done by friction and therefore causes a change in your mechanical energy as you sled down the hill. Work is equal to the force times distance traveled (W= F*d). Because friction is not a conservative force, it is path dependent (Serway and Jewett pg. 229). It doesn't matter where you go or how far, friction is always doing work on the system.
So there you have it. The forces that act on you when you sled are gravity, the normal force, and friction. The force of gravity pulls objects towards the center of the earth, the normal force acts perpendicular to the plane the object rests on, and friction which always acts against the the direction of motion, a non conservative force.


1. Main Page
2. The Projectile Motion of a Sled off a Jump
3. The Mechanics of Sledding
4. How Much Energy Does it Take to Sled?
5. Bibliography
Back to the sled. Another force that acts on the sled is friction. There are two types of friction, static and kinetic friction. Static friction is the resistive force that prevents an object from moving from a stationary position. The other type is kinetic friction which occurs when one object slides on another object (Feynman 12-4). The general equation for finding the force excerpted by the static and frictional force is F=µN. The µ symbol is the coefficient of friction which varies between 0 and 1. There is a subscript of either an f or s for µ when finding one or the other. (N) stands for the normal force which equals the mass in kilograms times the acceleration of gravity, 9.81m/s². Frictional force is a non conservative force and does work on a system. Friction causes a change in the mechanical energy of a system into internal energy and therefore is not conservative (Serway and Jewett pg. 229).
So, this means that, when you sled down a hill, there is a resistive force that works against you making you slow down and causes you to stop and the bottom of the hill. Work is being done by friction and therefore causes a change in your mechanical energy as you sled down the hill. Work is equal to the force times distance traveled (W= F*d). Because friction is not a conservative force, it is path dependent (Serway and Jewett pg. 229). It doesn't matter where you go or how far, friction is always doing work on the system.
So there you have it. The forces that act on you when you sled are gravity, the normal force, and friction. The force of gravity pulls objects towards the center of the earth, the normal force acts perpendicular to the plane the object rests on, and friction which always acts against the the direction of motion, a non conservative force.
Taken by Ryan Boothe
Taken by Jason Hoisington
1. Main Page
2. The Projectile Motion of a Sled off a Jump
3. The Mechanics of Sledding
4. How Much Energy Does it Take to Sled?
5. Bibliography