The Physics
This problem can be thought of as one of rotational motion due to force. As the wind pushes on the sail, the buoyant force and keel mass push in the opposite direction. So, if we can define all of the forces acting on the system, we should be able to say something about how the boat will react at certain wind speeds.
One problem in determining the wind speed necessary for capsize is the changing function of this system's center of mass, particularly the people inside. Most boat models involve boats that are much more massive than their passengers but mine will weigh around 75 lbs and carry 2 passengers. As the angle of heel increases, passengers can lean to compensate or not lean at all and, there will be a natural angle of capsize in which the passenger+boat mass would prefer inversion rather than correction.
My solution, as applied to this problem, was to basically remove the boat and passenger weight from the equation by assuming the axis of rotation to be the center of mass and, that they do not contribute a torque force. And, since the boat and passengers are most of the mass, adding a sail and keel would change the natural angle of capsize very little.
So my initial problem of wind speed necessary for capsize will be in terms of reaching that estimated angle at which capsize will occur or, simply one that is comfortable. This model can now be thought of as a simple problem of static equilibrium where, when the sum of the torques at an angle equals 0, v will be the wind velocity necessary to reach that angle.
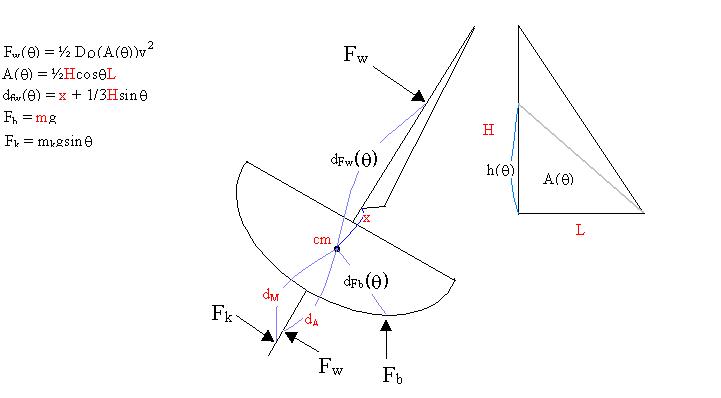
The diagram below outlines the torques exerted on the boat. Some distances are functions of the heel angle as well as the apparent area of the sail. I've noted in the red the constant values I have measured or specified. This model considers the worst case scenario of full sail directly on the beam.
This turns out to be a fairly straightforward problem of static equilibrium.
- Specify the estimated angle of capsize
- Set the sum of the torques equal to zero
- Solve for v
CHECK OUT THE FINAL CALCULATIONS!
![]()
 cover page
cover page