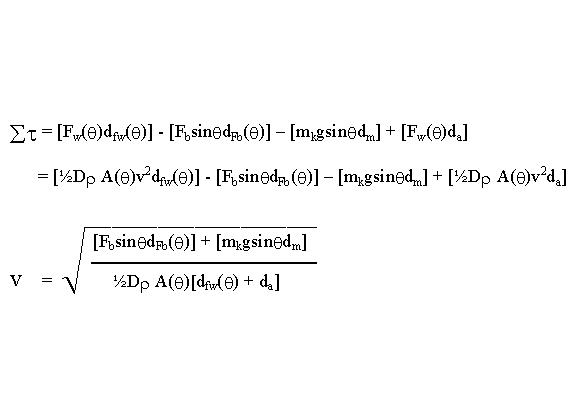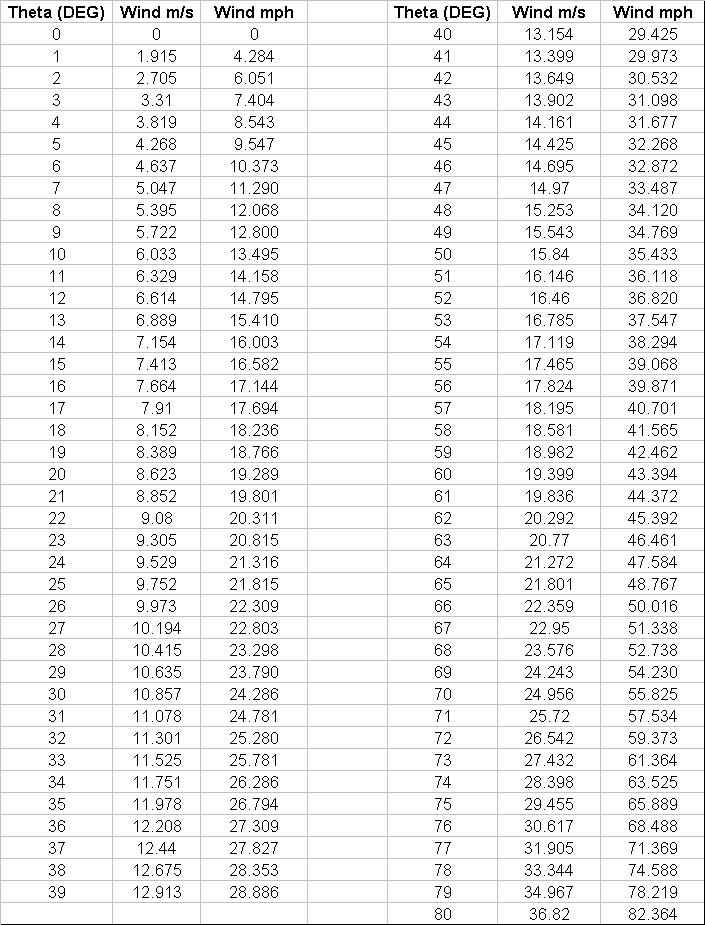
Calculations Values for forces and distances: the distance dfb of theta (above) is measured from a composite average of the boats mold sections, which are given in 2d plotted points all with a z location. I printed the average and then measured with a ruler for theta. The Sum of the Torque and solving for v: Feeding our V machine, here's values from theta through 80 degrees Where: D=2, H=1.2m, L=2.2m, x=.3m, Mass of the boat and passengers = 120kg, additional keel mass=10kg, dm=1.2m, da=1.2m, dfb = measured dfb Here's a fairly reputable stability calculation from The Cruising multihull, which is usually applied to monohull boats that are much more massive then their passengers. It predicts a high angle of capsize which I don't feel is necessarily valid in this model. Theta vs. Wind speed along with the value from the stability number As in all physical models, this model has associated error. I have not perormed the error analysis, and have made some approximate assumptions. In practice I will use these results as a rough guide to the stability. I find these calculations "seem" correct. In Kayakcraft, they give a stability plot of slightly shorter model and state that its maximum angle without capsize is around 58 degrees. I suspect my slightly longer boat could hold out at least as good. If this were the case, a wind speed of 41 mph would cause sure capsize. Now surely no one would ever want to get caught at 58 degrees in 41 mph winds in a kayak, but at least there's a window as to what the limits are. In all actuality, I don't think anything over 35 degrees in a kayak would be comfortable or dry. 27 mph winds would be required to heel to this angle. These particular calculations have a fairly small sail and light keel. The specifications of the final design are yet to be decided.

back to cover page