|
|
Kinetic & Potential Energy
|
| Without kinetic and potential energy cross country skiing would be extremely boring. There would not be the frustration of trying to maneuver up hill, only to slide down backwards in a failed attempt. Skiers would also miss out on screaming down those hills and crashing into a snow bank. Lets assume that energy is conserved when a cross country skier decides to conquer a mountain. When the skier is at the bottom of the hill their kinetic energy is at it's maximum and their potential energy is at zero. As the skier maneuvers up the hill their kinetic energy slowly decreases at the same rate that their potential energy increases. When the skier is halfway up the hill the kinetic and potential energies are equal. A few hours later when the skier has reached the top of the mountain, their potential energy is at its maximum and their kinetic energy is zero. Kinetic energy is one half times the mass times the velocity squared. Kinetic energy = 1/2mv2. Potential energy is the mass times gravity times the height. Potential Energy = m*g*h. Conservation of energy states that Ki + Pi = Kf + Pf. This simply means that the sum of the skiers initial potential and kinetic energy is equal to the sum of the skiers final potential and kinetic energy. With the potential energy at its maximum the skier decides to risk it all and descend. Mirroring the effects of climbing the hill, the skier slowly loses potential energy the farther down the hill the skier is. This causes the skier's kinetic energy to increase, as predicted by conservation of energy. When the skier is at the bottom of the hill, the potential energy has dropped to zero and kinetic energy is once again at its maximum. Depending on the friction of the snow on the skier, the skier would slow down and come to a rest sometime after reaching the bottom of the hill. The animation below illustrates this concept very well. As the skier goes down the hill, the Kinetic Energy, Potential Energy, Work, and Total Mechanical Energy bars reflect what is happening in the system. 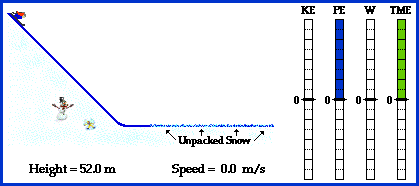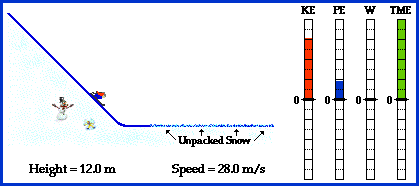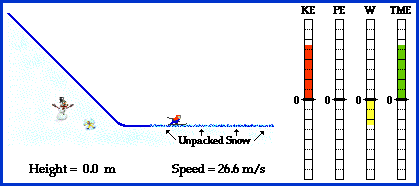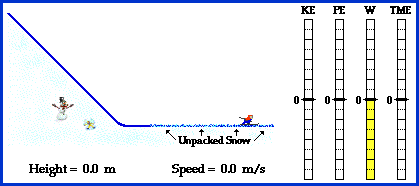
http://www.physicsclassroom.com/mmedia/energy/se.html
There are some flaws in the ideal scenario above.
Cross-country skiers are constantly effected by friction which is not
a conservative force. Air resistance and the use of poles are also
factors which effect conservation of energy. Despite these outside
influences, the animation above still gives a general idea of what happens
to work and energy when a skier goes down hill.
|