Light
Refraction
As
was mentioned with the refracting telescope in optical
paths, the index of refraction determines the way that
the primary objective lens will be created, as well as its
dimensions (such as the thickness and curvature of the glass
platelet). The index of refraction of a material is determined
by the ratio of the speed of light in a vacuum to that of
the speed of light in the material that the light is passing
through, or n = c/v (The Refraction of Light Part II).
The
angle of incidence and the angle of refraction are related
to one another by the formula sin(angle2)/sin(angle1) =
c/v, or the refracted angle over the angle of incidence
equals the speed of light in a vacuum over the speed of
light in the material (i.e. the index of refraction). A
simple diagram of the refraction of light through a solid
flat surface can be seen below.
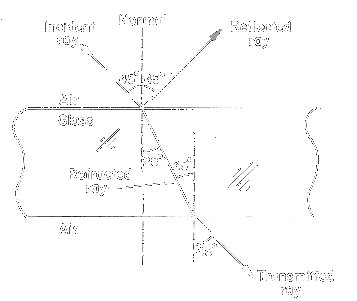
Image courtesy of The
Refraction of Light Part II
As
you can see the light is being "bent" when it
hits the glass and exits at the same angle that it entered.
In fact, the only thing different about the transmitted
ray is that it's shifted a bit to the left (and ultimately
it's magnitude has been reduced because of the precense
of the reflected ray, which is very dim).
As
you have probably noticed, a flat piece of glass is not
very useful for telescope optics that need to focus light
at a central point. So in order to get the light to bend
through the glass so that it can be focused into a spot
where an eyepiece can intercept it, as is the case with
a refracting telescope, the glass must be curved. This curvature
changes the angle at which the light hits the glass at every
point along its surface. This "angle of incidence", as it
is called, is determined by the normal line to tangent line
on the surface of the glass at any point along its surface
where light hits it. This allows the light to have different
angles of refraction and therefore different angles of transmission,
making it possible to force the light into a cone and ultimately
into a point. A crude one element lens example for
the lens of a refracting telescope can be seen below with
respective angles.
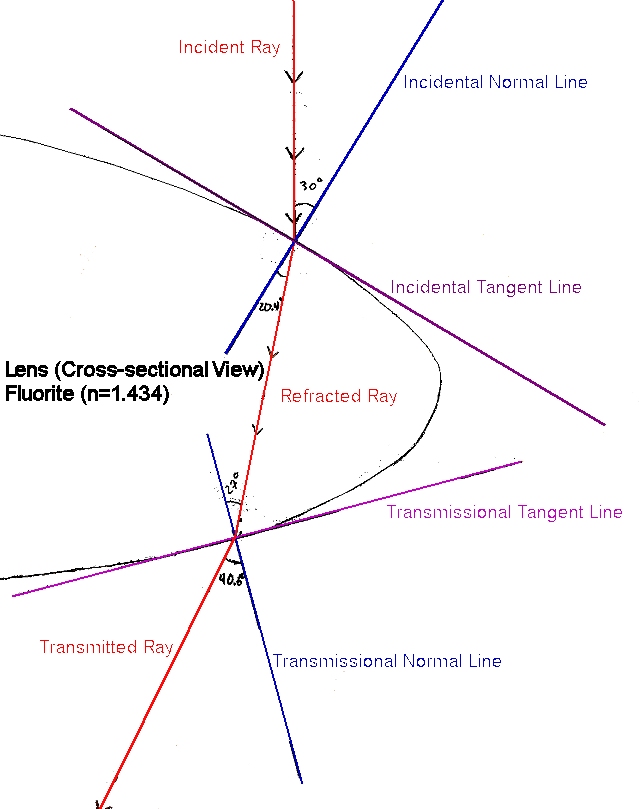
In
the diagram above, the glass used for this hypothetical
lens is that of Fluorite and is assumed to be gathering
light in an environment surrounded by air. The equation
utilized to calculate the angle of refraction when the angle
of incidence is known is from the equation
n1*sin(theta1)
= n2*sin(theta2) (eq.1)
where n1 is the index of refraction of the first medium
which is, in this case, the index of refraction of air (1.0003),
n2 is the index of refraction of the second medium that
the ray enters into which, in this case, is Fluorite (1.434),
and theta 1 is the angle of incidence (30 degrees). Hence,
solving the following equation
(1.0003*sin(30))
= (1.434*sin(theta2))
for theta2 will yield the angle of refraction of 20.4 degrees.
Once this has been done, the final angle of transmission
can be easily calculated by determining where the refracted
light beam will arrive at the other side of the lens. This
will yield a new tangent line and normal line which will
yield a new angle of incidence (27 degrees). The procedure
for finding the final angle of transmission is exactly that
of the one listed above to find the angle of refraction.
Plugging in the known variables into equation 1 will yield
(1.434*sin(27))
= (1.0003*sin(theta2))
Solving for theta gives a final transmission angle of 40.6
degrees from the normal line. This makes sense, as the angle
of the light would then be bent towards the central optical
axis (inwardly) towards a common center (i.e. towards the
focal point/eye piece). This is exactly how a refracting
telescope lens works, and it is truly a fascinating topic.