Daniel Lenord
University of Alaska Fairbanks
Physics 211 Web Project, Fall 2002
| Index | 100-meter Dash | Javelin | Pole Vault | Bibliography | |
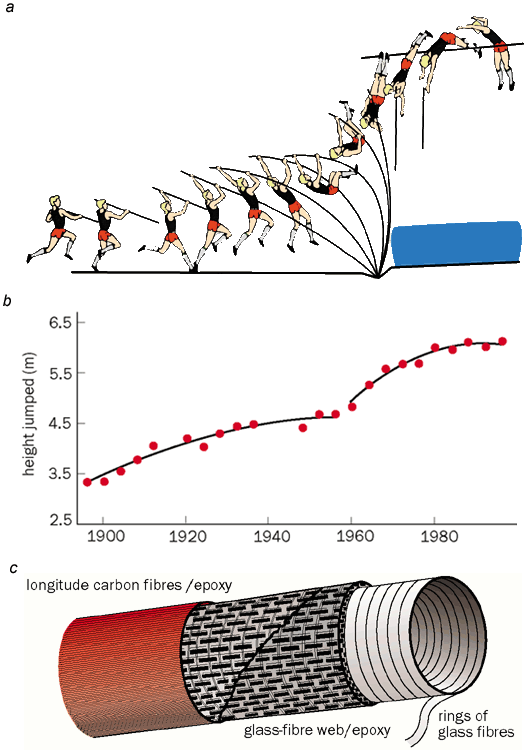
An example of a pole vault
The rules for pole-vaulting that are set by the International Amateur Athletic Federation (IAAF) - the sport's governing body - are extremely liberal. There is no restriction on the length of the pole, the materials from which it is constructed or its energy-storage capacity. The only stipulation is that poles should be generally smooth and not be covered with too much adhesive tape.
Poles were originally made out of solid wood, probably hickory. Slightly more flexible bamboo poles were introduced in the early 1900s, mostly by American vaulters, who dominated the sport at the time. Basic mechanics tells us that the highest stresses occur on the outside of a bent beam, and that a symmetrically bent object, such as a pole, actually has a zone down the middle (known as the neutral axis) where the stresses are very low and even zero. There is therefore no need for the pole to have any mass down the centre. Bamboo, which is a naturally hollow material, is much lighter per unit length than a solid pole - yet provides the same maximum stress. This enables an athlete carrying a bamboo pole to either take a faster run-up or to use a slightly longer pole.
Essentially pole-vaulting involves the conversion of the kinetic energy of the running athlete to the potential energy of the jump using strain energy stored in the pole (the energy stored in elastic deformation). Consider an athlete of mass m = 80 kg running at a speed v = 10 m s-1, who has kinetic energy of 1/2mv2 = 4000 J. If this energy is converted with 100% efficiency into potential energy mgh, where g is the acceleration due to gravity and h is the height jumped, then the athlete can climb a height of 4000/mg, or just over 5 m. However, in reality, most pole-vaulters can jump heights of nearly 6 m. So where does the extra energy required to propel the athlete to these greater heights come from?
It turns out that the extra energy comes from the athleticism of the vaulter bending the pole. Energy is stored in the pole as it is bent or strained by the athlete's muscles, and returned to the vaulter as the pole recoils. The strain energy comes from the work done by the muscles of the athlete as he or she takes off, carrying out work on the pole as it is bent. The maximum strain energy of the pole is ms2/2rE, where s is the maximum or "failure" stress on the outside of the pole, r is its density and E is its Young's modulus (i.e. its "stiffness").
Clearly, pole-vaulting is an example of a sport in which technology has been used to improve athletic performance. As the Olympic winning heights in the discipline level off, it will be interesting to see if our ingenuity can provide another technological leap to allow pole-vaulters to jump even higher.
