Introduction

Acceleration

Drag Force

Terminal
Velocity

Links

Bibliography

Acceleration Due To Gravity

Why does a skydiver accelerate as he leaps from the plane? The answer to this question is relatively simple: gravity. Gravity acts on all bodies in the universe, and each bodies' gravitional effects are related. The body that the majority of the human population is affected by is the planet earth. The gravitational acceleration produced from earth is approximately 9.8 m/s^2, which changes slightly as you move closer to or away from the earth's center of mass.

Lets examine an instance for which a person named Joe prepairs for his first skydiving experience. Joe gets on a plane with an instructor and heads towards the sky.

First off, while Joe is in the plane, he does not constantly accelerate downward, assuming the altitude of the plane remains constant. Why might this be the case? Newton's Second Law states, "The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass" (Serway et al). Therefore, we know that if there is no force acting on a body, the acceleration of the body is equal to 0. Lets examine a free body diagram of this situation.

Where M is equal to Joe's mass and G is equal to Joe's acceleration from Gravity. Fplane is equal to the normal force, which balances out the downward force of Joe.

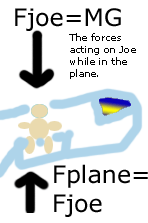
One may now clearly see why Joe does not accelerate downward while he remains is in the plane. The normal force of the plane is acting against the normal force of the gravity acting on Joe's 100 kilogram mass (this is getting close to the maximum weight allowed for skydiving). Since the sum of the forces in the y, or upward direction, is equal to zero, there is effectively no force acting on Joe. Thus, the acceleration of Joe must be zero.

Now that Joe understands why he is remaining at a constant altitude, he's ready to take his first jump. Joe is given the signal to jump from the jump master, and he steps right off the edge of the plane. Joe is now instantly accelerating in the downward direction. Joe's acceleration will soon cause him to travel at a rapid rate. But exactly how fast will he be traveling at a certain time? Without this knowledge, Joe could easily splatter against the surface of the earth. In order to calculate Joe's velocity at any time, T, we use the following equation:

X = Vi * T + .5 * g * t^2

Where X is the change in distance, Vi is the initial velocity, t is time, and g is the acceleration due to gravity. Since we know Joe's initial velocity was 0, and the acceleration of gravity is always 9.8 m/s^2, we can calculate how far Joe has traveled at any point in time. Lets examine the new free body diagram for this situation.