Blood flow has Kinetic energy, and:

E = KE + PE

              Marxen et al. (2006).

As an artery branches into smaller arteries, with half the diameter of the artery previous, what happens to the velocity of the second relative to the first branch, and so on? Velocity will double, according to the caution of continuity.

ρ A₁ v₁ = ρ A₂ v₂

A₁ v₁ = A₂ v₂

Because rho (density) drops out!

An ideal fluid moving through a blood vessel is considered to be non-viscous and incompressible, with no rotational motion i.e. flow is laminar or streamlined.

Flowing blood has kinetic energy (KE), and KE is proportional to the mean velocity squared. Blood flowing in a vessel is subject to pressures exerted by the endothelial lining, which can change based on changes in cross sectional area. The total energy flowing in a blood vessels is therefore equated with its kinetic energy, plus potential energy (PE).

Blood flow is driven by differences in pressure. Also, changes in kinetic energy affect changes in potential energy, with: E = KE(initial) + PE(initial) = KE(final) + PE(final). For example, is a skier runs down a slope, potential energy (U = mgh) is converted to kinetic energy (KE), at the bottom of the hill.
This is the basis of Bernoulli's principle. Let's consider a blood vessel that narrows before it returns to its original diameter.

Velocity decreases as the cross sectional area of the blood vessel decreases. Imagine this figure as a constriction in a blood vessel.

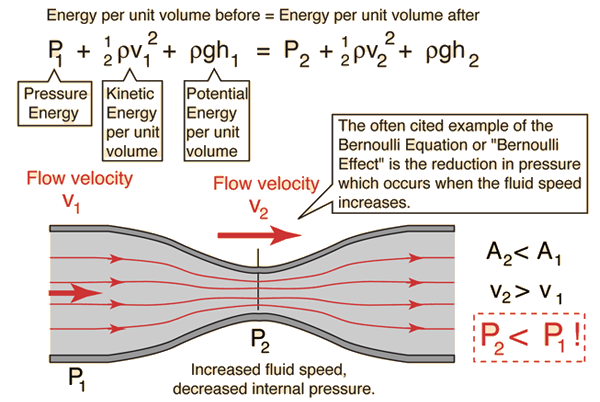Image credit: hyperphysics.phy-astr.gsu.edu



This equation can seem counter intuitive; however, if you consider pressure like "energy density", a higher velocity at a point of constriciton relative to a bigger cross sectional area means kinetic energy increases at the expense of a decrease in pressure energy (P).

If a person has arteriosclerosis, then Bernoulli's principle can explain the pathology of a vascular flutter. An artery may be constricted by the accumulation of plaque along the endothelial wall. The external (driving) pressure must increase in order to drive a constant flow rate through the constriction (where an increase in fluid speed = a decrease in internal pressure).  This results in a greater demand on the heart muscle relative to the non-diseased state. A flow rate that is sufficient high at the point of constriction can cause the collapse of an artery due to the corresponding high external pressure (P1 in the figure above). 

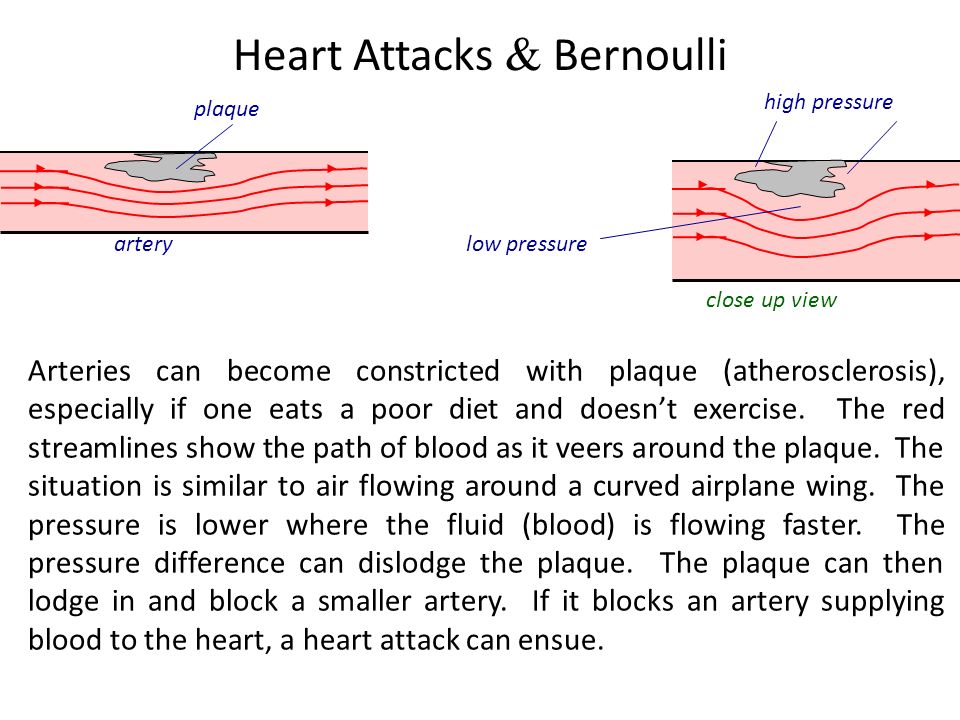Image credit: Y. E . Gunanto

The study of physics, itself, need not be stressful; remember the importance of a healthy diet, rest, and exercise.