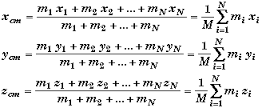Center
of mass (CoM),
while not the most interesting topic in physics, it is very
important to the movement of a figure skater. As stated before
skaters must keep their CoM
directly over their ice skates or base of support. If they do
not keep their CoM
over their base of support they will become off balance and will
fall flat on the ice. A figure skater generally doesn’t have too much
difficulty with keeping their feet underneath them during
routine movements, but more complicated movements such as jumps
or spins require more thought.
Spins
In circular motion, center of mass is a point on the object that remains motionless while every other part of the object is undergoing circular motion around that point. A figure skating performing a spin is a perfect example of rotation about the center of mass. The blade of a figure skate is specially designed to help improve skating movements such as edges, jumps, and especially spins. On a figure skate blade there is a special spot called the spin rocker. It is located near the front of the blade, nearly right behind the toe pick. The spin rocker is a “sweet spot” that the skater looks for while trying to center up a spin. When you are properly located on your spin rocker, the spinning rotations will feel easy without a lot of scratching noise caused by other locations on the blade, like the edge or toe pick. A figure skaters center of mass comes into play here when they are trying to center a spin. If a skater is doing an upright scratch spin, their CoM should naturally be over their base of support. However, if a skater is performing a sit spin, the arrangement of their body mass has been changed, they must now lean forward slightly to counteract the mass of their foot and hands reaching out in front of them. If the skater cannot balance their CoM during a sit spin they will end up with a wobbly and off center spin , something that is not very pleasing to the eye!
The image below illustrates the correct and incorrect print of a spin. If the spin is not centered the skater will be sent off in spiraling loops, but if it is well centered, the skater will leave perfect circles on the ice.

Jumps
Performing
a
figure skating jump is truly exciting! But can be even more
exciting, and not in a good way, if you are improperly executing
the jump. Most jumps done by figure skaters require some sort of
rotation, it could be one rotation or it could be four. As it
was with spins, the importance of CoM
to rotational motion is just as important here. Maybe even more
important because jumps also have another element of height,
thus the consequences of an off center rotation would likely be
much more painful! Without going into the complications of
entering a jump, once a skater leaves the ice and starts their
projectile motion, they must immediately center their mass,
arms, legs, head, hips over their base of stability (i.e.
landing leg/foot). Figure skaters do this by achieving a
somewhat corkscrew like shape where their arms are crossed
across their chest and their legs are crossed at the ankles or
shins, take off leg over landing leg. If a skater cannot center
their mass over their landing leg during that split second in
the air, they will most likely not land the jump. The image
below, on the left, illustrates the proper alignment of this
skaters CoM, as you can see it is directly over her landing leg
in preparation for a smooth follow out. The image on the right
is not a true or technical representation of where Sasha Cohen's
CoM is, but clearly her jump did not go well..Ouch!


If we felt like getting more in depth...
We could actually
estimate a skaters center of mass if we modeled her as a rigid
body where her mass distribution is not constantly changing. We
would do this by using the following equation and the distances
and masses of her extremities and then we would calculate her CoM
in three directions, the x, y and z directions. Xcm can also be
thought of as the average CoM in the x coordinate. Same applies
for Ycm and Zcm.