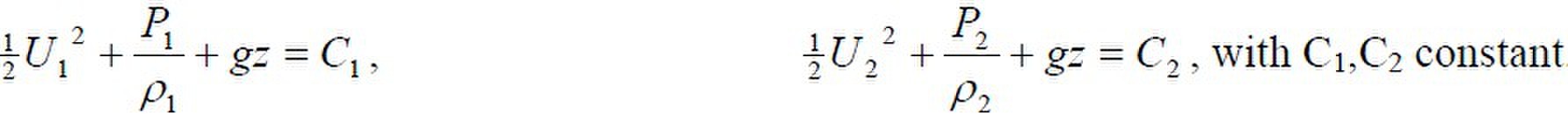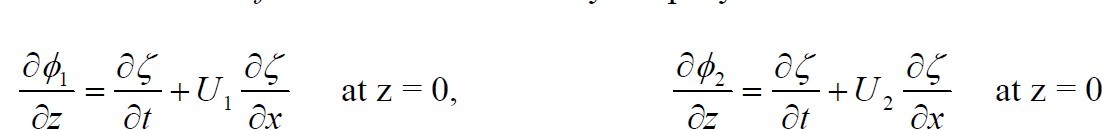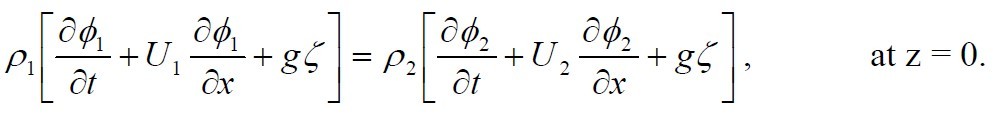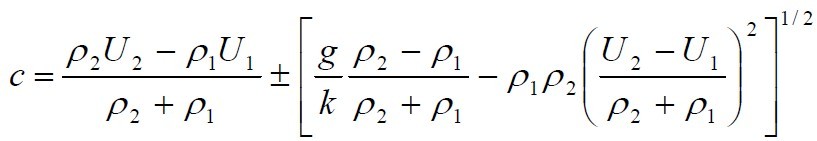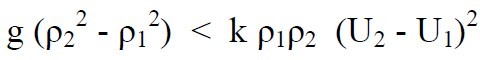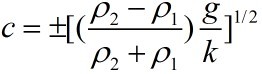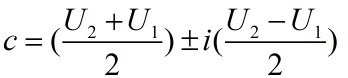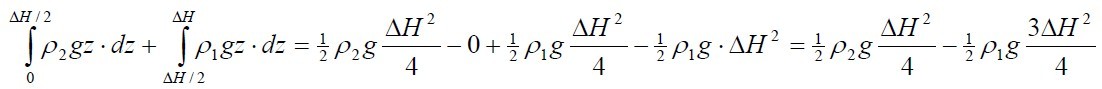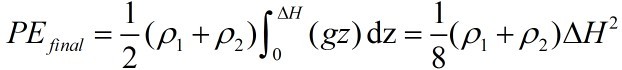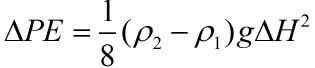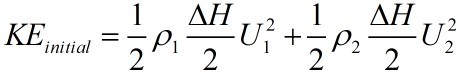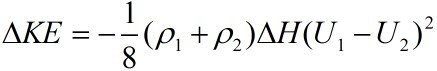Discontinuous condition
-two flows with
different velocities
1, Basic Equations
At
first, we consider a two-layer system, with perturbation
added at the interface between two fluids with different
velocities. We'll try to derive the momentum equations of
fluid under the assumptions
we mentioned before. Under those conditions,the momentum
equations become:
For
barotropic motions (ρ ≡ ρ(p)) like that we study, the
momentum equations lead to:
in
which q=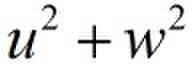
,and 
,
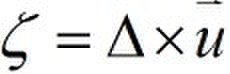which is the vorticity.For a irrotational system, the right
hand side of the equations become 0. Then the equations lead
to:
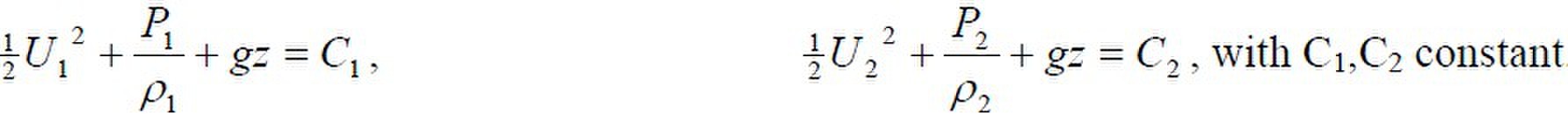
which are the Bernoulli equations.
2, Add Perturbation
Then we add a perturbation to the system, which can
be characterized by two-dimensional velocity potential
functions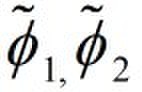 
within each region:
After a lot of math(for more details,please see Lew
Gramer Sec 4), we get the unsteady Bernoulli
Equation:
3, Boundary
Conditions
There are four boundary conditions:
=
=
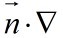
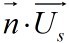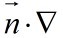
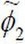on z=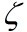
and P1=P1 on z=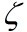
Using these boundary conditions, after some
math( see Kundu Sec 11.3), we can get
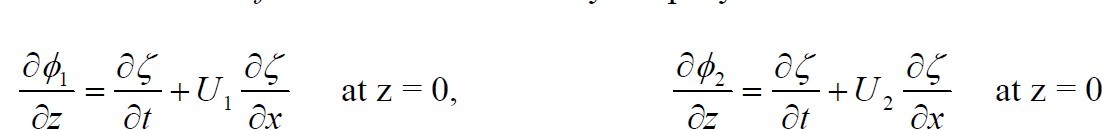
which is eq. 11.9 in Kundu and
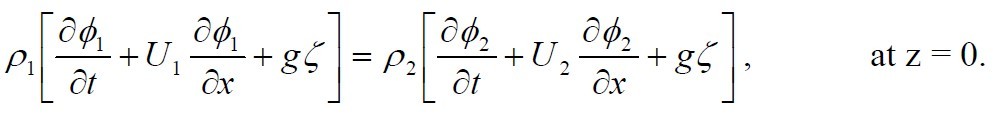
which is eq. 11.13 in Kundu.
4, Solutions
Now assume that the solutions for , 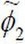have exponential form,
namely,
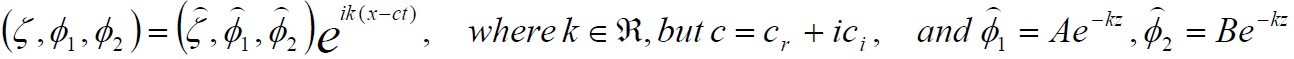
Plug those forms into the equations we got using the
boundary conditions( see Kundu Sec. 11.3), we can
get the solutions for c are:
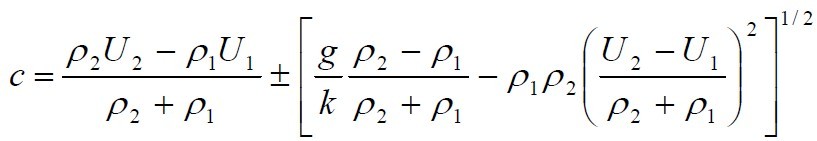
5, Analysis
Given the solutions for c, we can analyze the
stability of the system. Obviously, when
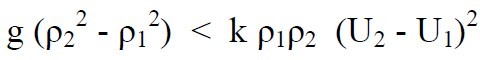
the system is unstable. This means that when the velocity
difference is large enough, density
difference is small enough, or wave
number k is large enough, the system
is unstable.
1), When U1=U2, the solutions get simplified,
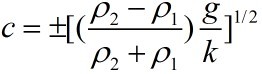
which means
when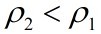 
, the system is unstable.
That's called Rayleigh-Taylor instability.
2), When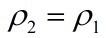 
, the interface becomes a
vortex sheet. The solution becomes
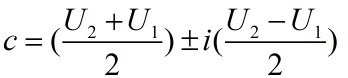
Which means
that vortex sheet is always unstable to
disturbances of any wavelength.
3), Generally speaking, for a given velocity
difference, no matter how small it is, there always
exist
a wave number k that
makes the system unstable. In another word,
for short wave disturbances,
the system is always
unstable.
We can use
the figure below to illustrate the whole progress.
(Figure from Kundu)
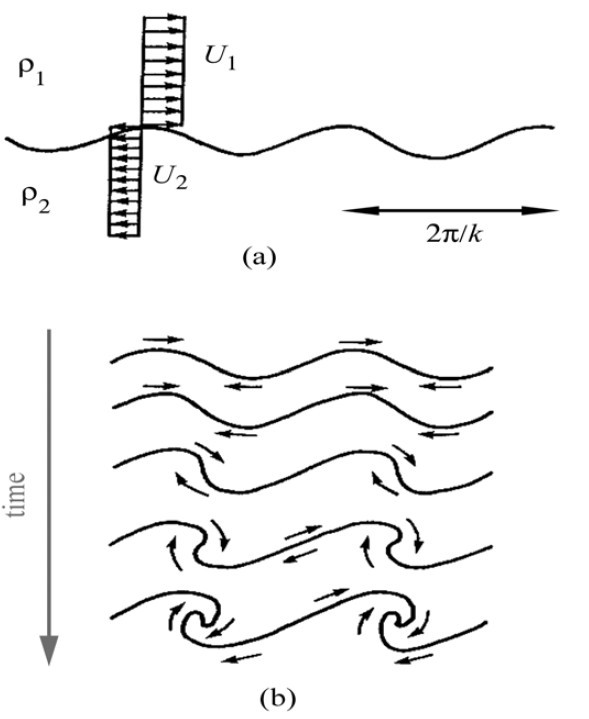
6, Transmission
of Energy
The source of energy to generate the K-H instability
is derived from the kinetic energy of the two
steams. This progress can be illustrated by the
figure below.(Figure from Gramer)
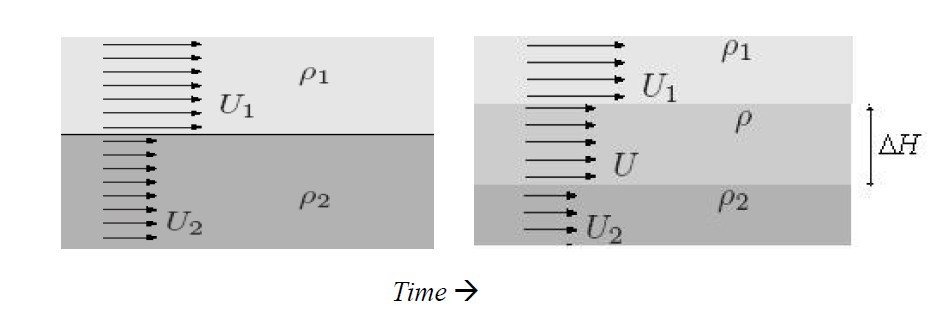
From the figure we can get:
The potential energy of the initial state
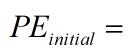
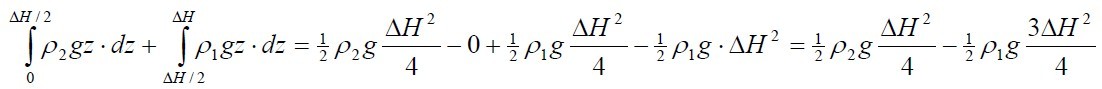
The potential energy of the final state
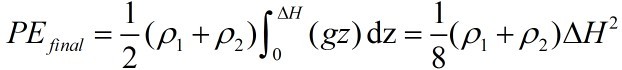
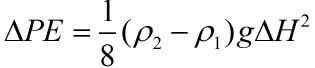
The kinetic energy
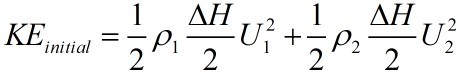
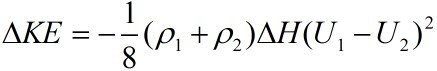
Therefore, the kinetic energy of the system
decreases while the potential energy increases.