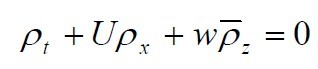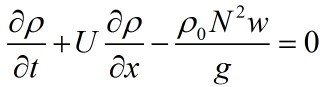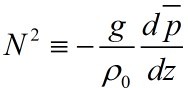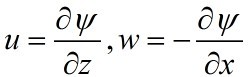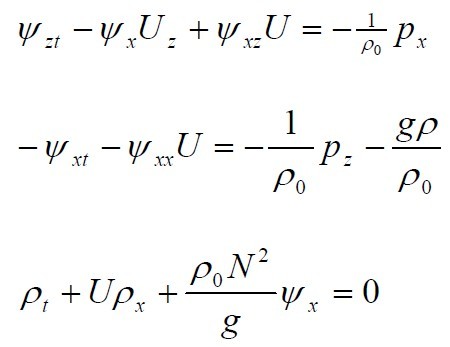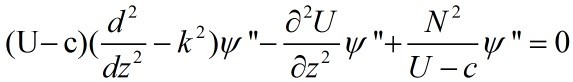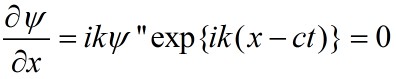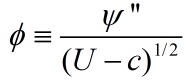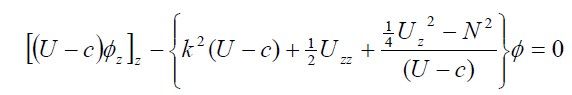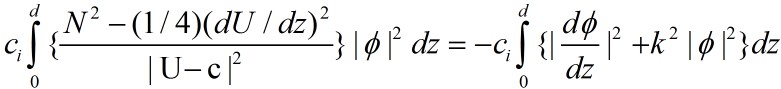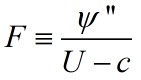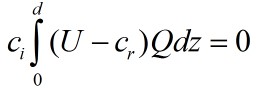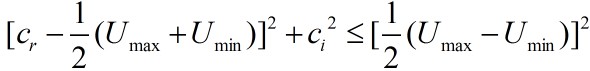Instability of Continuously Stratified Parallel Flows

1,Taylor-Goldstein Equation

2,The Gradient Richardson Number

3,The behavior of the phase speed c

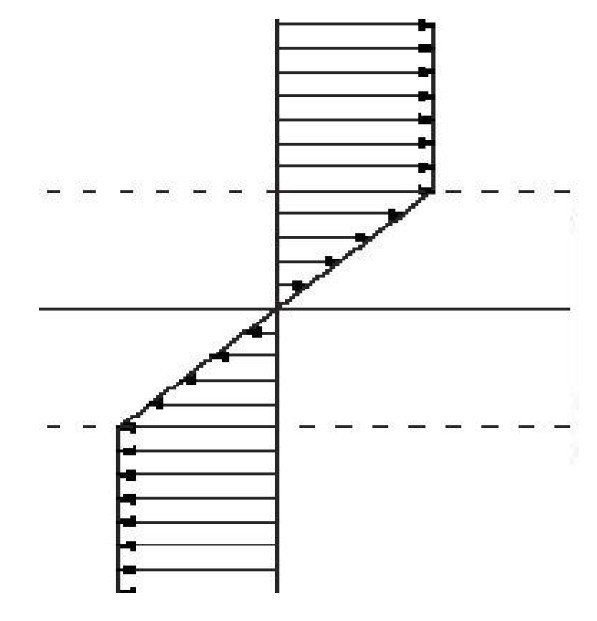
We assume a basic state of a continuous stratified parallel flows, which can be illustrated by the figure below.
                                             figure5_Crushman-Roisin
1,Taylor-Goldstein Equation
Assume the basic state can be characterized by U,P and 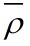symbol6. Then we add a disturbance to the system. Then the system can be characterized by
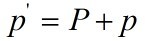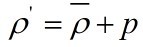
                      ,equation27 and equation29
As we assumed before,  the momentum equations become:
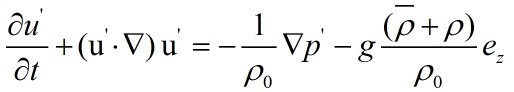
                     equation30
The basic state satisfies:

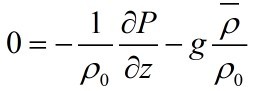
                      equation30
Here 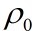symbol7 is a reference density. Subtracting the last two equations and dropping nonlinear terms ,we get:

                      eq32
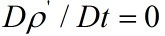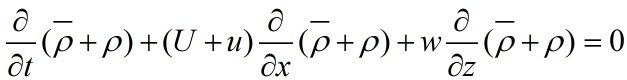Using equation33, or equation34.

Drop nonlinear terms ,we get

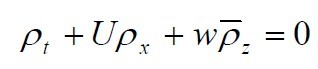
                    equation35
Which can be written as
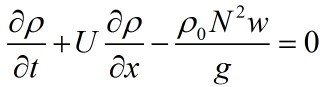
           equation36
in which N is the buoyancy frequency of the flow:

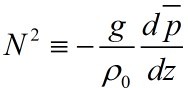
             equation37
To meet the continuity equation, we assume a stream function 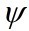symbol8, which satisfies

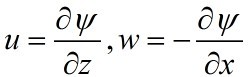
                            equation38

Then then equations we got before can be written as

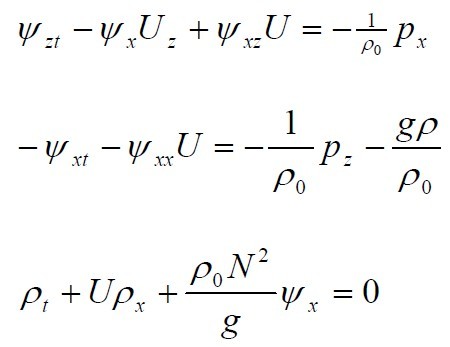
                         equation39
Since the coefficients in these equations are independent of x and t, we can assume that the solutions have the form of


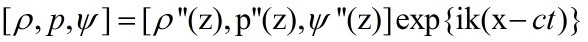
                            equation40
             
After some elimination, we can get the equation for symbol8:

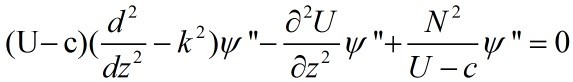
                           equation41

This is the Taylor-Goldstein equation

2, The Gradient Richardson Number

Since the property of the Taylor-Goldstein equation, a nonzero ci ensures instability. (see Kundu Sec. 11.7)
The boundary conditions are what w=0 on rigid boundaries, namely z=0 and z=d. This means that
 
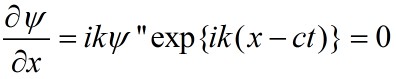
                            equation42

namely

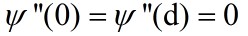
                                  equation43
 
Define a new field variable 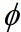symbol9  by

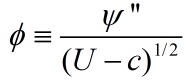
                            equation44

After a series of math, the Taylor-Goldstein equation becomes(See Kundu Sec. 11.7)

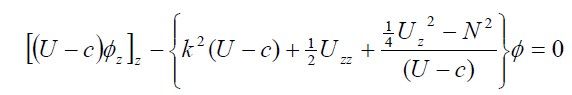
                        equation45

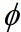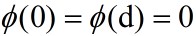Multiply this equation by symbol10, which is the complex conjugate of symbol9, integrate from z=0 to z=d,and use the boundary conditions equation46, we can obtain:

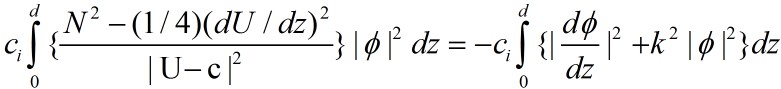
                             equation47

Obviously, the integral on the right hand side is positive. If 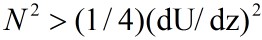equation48 everywhere, then ci times a positive value equals -ci times a positive value. That means ci=0, which indicates that the system is stable. So define the gradient Richardson Number:

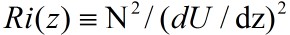
                           equation49

We say stability is guaranteed if:

                            Ri>(1/4)

We need to point out that the criterion doesn't guarantee that the flow is unstable if Ri<(1/4) somewhere ,or even everywhere. So Ri<(1/4) is a necessary but not sufficent condition for instability. Actually, there is no unique lower boundary of Richardson Number that guarantee instability for all distributions of U(z) and N(z).

3, The behavior of the phase speed c

Similar to previous analsis, but define a different field variable F by:

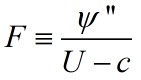
                       equation50
 
we can get

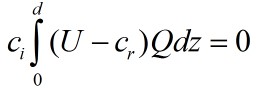
                      equation51

in which

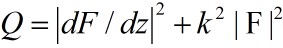
                       equation52

For instability, Ci is nonzero. That means (U-Cr) must change sign somewhere:

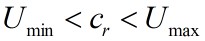
                      equation53
whice means that Cr lies in the range of U. Since Cr is the phase velocity in the positive x direction. The inequality above means that Cr is positive if U is positive everywhere and negative if U is negative everywhere.

We can also get the properties of Ci. According to Kundu Sec. 11.7, Ci satisfies:

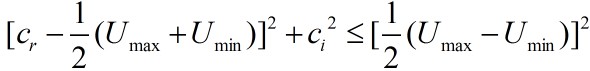
                         equation54

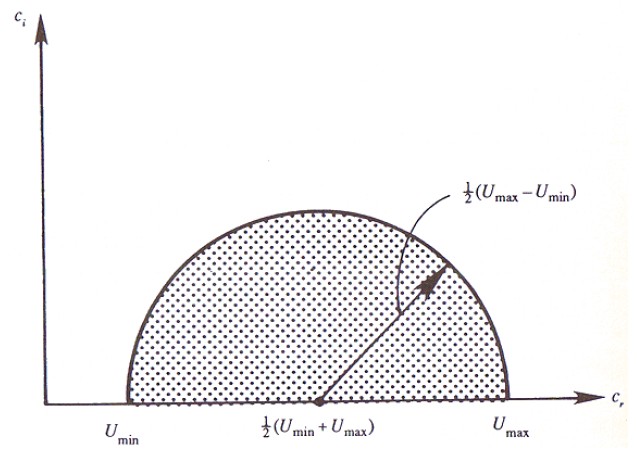
This relation is first derived by Howard (1961), so it's called Howard semi-circle theorem.It can be illustrated by the figure below (pitcure from Kundu Sec. 11.7)

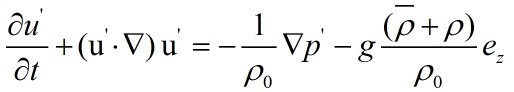
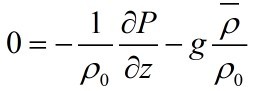
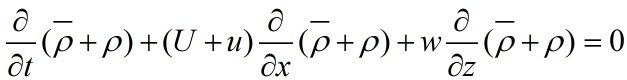                                               figure6_Kundu