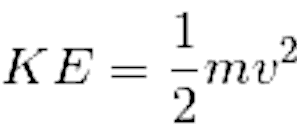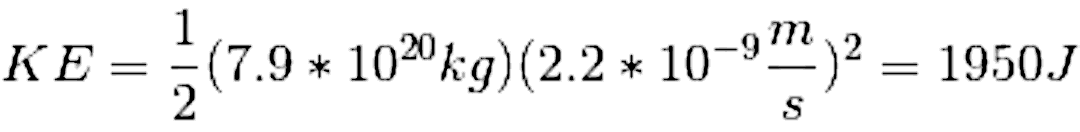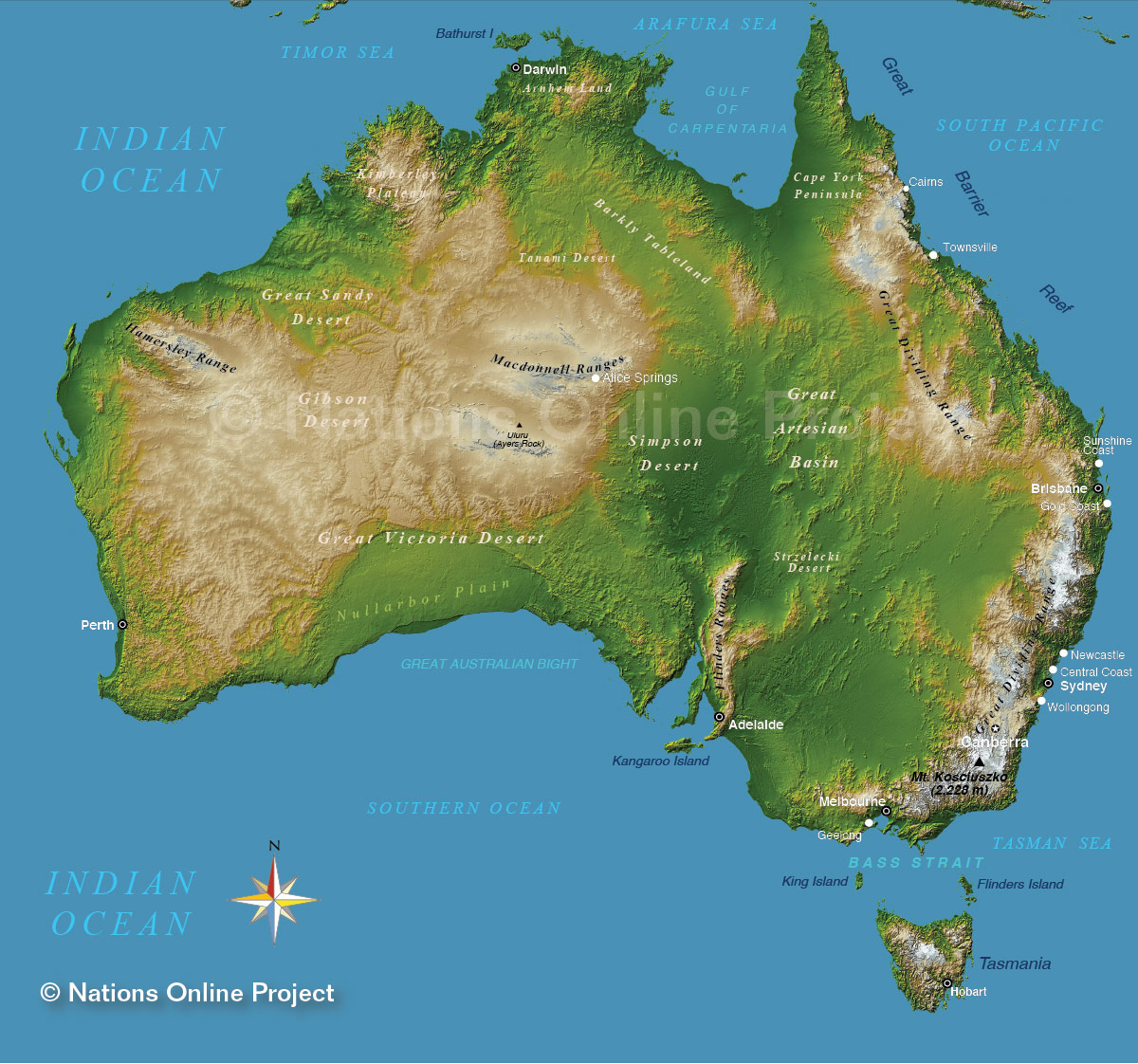
Kinetic Energy of a Continent So how much energy is there in continental drift anyway? Energy can be invested into the crust in many ways, such as potential energy in large mountain ranges, kinetic energy in the movement of plates, and elastic energy caused by compression of the plates. The easiest of these to solve for is kinetic energy. Kinetic energy is solved using the equation KE=1/2mv^2. We will solve for the kinetic energy of Australia, because out of every continent, Australia is the least geologically active at its center, and as a result its movement is very uniform. 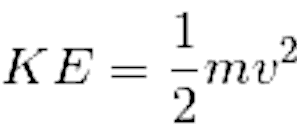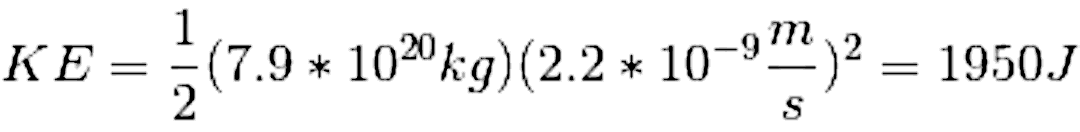According to Clitheroe et al, the crust of Australia is 38.8 km thick on average. Multiplied by an area of 7.69 million km^2, the continent of Australia has a volume of 2.98x10^17 m^3. A typical felsic rock has a density of 2650 kg/m^3 (West). Thus the continent of Australia has a mass of 7.9*10^20 kg. According to Howard, the continent of Australia is drifting northward uniformly at 7 cm per year, or 2.2^10-9 m/s. Since we have v and m, we can solve for KE. This comes out to 1950 joules. 1950 joules is a very small amount of energy. There is much uncertainty in this number, such as the assumption that all of Australia is felsic material. Another important factor to consider is that this accounts only for the kinetic energy of the portion of the Australian continent that is above water, while a very large portion of it resides underwater. It is clear however that the magnitude of Australia's kinetic energy is very small. This does not, however, mean that there is little energy in continental drift. Continental drift causes huge releases of energy such as earthquakes and volcanic eruptions. It simply means that little of this energy is stored as kinetic energy. Other ways that energy can be stored in the crust are as thermal energy, elastic energy caused by compression of the crust, and as potential energy, such as when forming mountain ranges.