its not what you're thinking

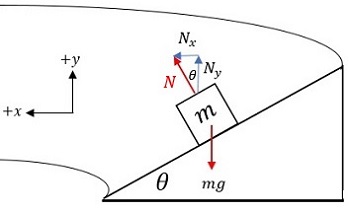
Matthew Bergstresser states in his lesson, " A mass moving in a circular path on a flat surface requires friction. If that surface is banked, the mass can move in a circular path without friction, but only if the conditions are optimal" (https://study.com/academy/lesson/circular-motion-around-a-banked-circular-track.html). What are these optional conditions?

copyright @ Matthew Bergstresser | study.com
Using Newton's second law, we can derive the formula tan = v ² / g r .
In this scenario, theta is the banking, v is velocity (which must stay CONSTANT), g is gravity, and r is the radius of the curve that the mass is going around. Note that this formula gives an angle of banking for a specific, unchanging velocity, if acceleration is occurring or the velocity is not the correct constant, friction is again required to keep the car on the road.

According to Doug Davis, "A banked curve is designed for one specific speed. If the banked curve is icy so there is no friction force at all then traveling at higher than design speed means the car will slide out, up, and over the edge and traveling at lower than design speed means the car will slide in, down, and off the bank" (http://www.ux1.eiu.edu/~cfadd/1150/05UCMGrav/Curve.html).

Banking on race tracks helps a driver not only turn with more ease, but also maintain a greater connection from the tire to the road.


copyright @HEFFX