Real life example

2017-04-14 ,  Jan Cech, 

Example of energy transformation

Non ideal condition

   In real life, the energy is not conserved. Energy loss occur because of friction between skis and snow. To prevent that, skiers wax their ski chambers with paraffin waxes, which repel water molecules in snow and reduce then the friction coefficient. Another way how to get closer to ideal skier, is aerodynamic spandes which helps improve the air flow due lower air resistance. Skier uses various for minimalizing the energy loses, skier wax their skis and wear slim spandex, so their skis have smaller friction during the contact with snow and their spandex makes them more aerodynamic.

Ideal condition example

    In real world, we deal with lots of variables in downhill skiing. For our example purpose, we will neglect air resistance and friction between skis and snow. This brings us to ideal problem, when energy in system is conserved between potential and kinetic energy, Ep and Ek respectively

Equation for energy transformation:

Ep(initial) + Ek(initial) = Ep(final) + Ek(final)

Equation for gravitational potential energy:

Ep = mass * g * height

Equation for gravitational kinetic energy:

Ek = 0.5 * mass * (speed)^2

Picture downloaded from

http://www.real-world-physics-problems.com/physics-of-skiing.html

Example
Skier with weight 70kg skis down the ski slope, which start gate altitude is 1000 m above the sea level and altitude at the bottom of the hill (in finish) is 900 m above the sea level.
A)    How does skier potential energy transform into kinetic energy during downhill ride?

B)    What will his speed be when he crosses the finish line?

m = 70 kg

Altitude at the top of the hill = 1000 m above the sea.

Altitude at the bottom of the hill = 900 m above the sea level.

We consider no air resistance and frictionless contact between skis and snow.

Solution:
A)
Ep(initial) + Ek(initial) = Ep(final) + Ek(final)

Ek(initial) = 0

Ep(final) = 0               =>              Ep(initial)  = Ke(final)

Ep(initial) = mass * g * height = 70 kg * 9.8 m/s2 * (1000-900m) = 68,600 J
Ek(final) = 68,600 J = 68.6 KJ

B)
Ek(final) = 0.5 * mass * (speed)^2 =>

velocity = (2*Ek/mass )^0.5 = (2*68,600 J /70 kg)^0.5 = 44.3 m/s
To imagine the speed better, we can convert it to miles per hour.
v(MPH) = (44.3 m/s)*(1mile/1609m)*(3600s/hr) = 99.1 MPH

There is graph, below, showing change in energies (assuming constant slope)

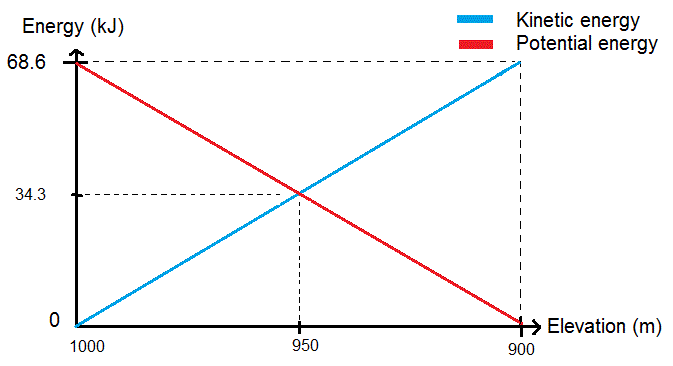
Graph made by Jan Cech

Conclusion
    To be honest our example was ideal, in real world, skiers reach similar speed, but they need higher hills to reach the speed. Also in real world, the horizontal distance plays its roles as well and the energy is not conserve, while the speed not only depends on the elevation of race course, but also the horizontal distance. Shorter and steeper hills give skiers higher velocity, because the friction (due to normal force) is smaller, than for more flat course with same elevation. Also in real world the friction coefficient increases with duration of race, because the waxed layer on skis is getting thinner. We also assumed that skier did not turn the whole time, so he did not lose any kinetic energy for turns.

Support for my ideas comes from
http://www.physicsclassroom.com/class/newtlaws/Lesson-2/Types-of-Forces