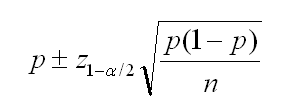Probability in Physics

Trace Braxling
Physics 212 F09

What is Probability?

When someone flips a fair coin, it is said that it has a 50% change of landing heads, and a 50% chance of landing tails. But what does this mean? The way that a coin lands can be calculated. A machine can be built that flips a particular coin in a particular way so that it lands on an exact face every single time. So why do we determine possible outcomes by percentage probability? It may be relatively easy to calculate the outcome of one coin flip, but what about 100 coin flips? 1000? 1,000,000? At a certain point, calculating the outcome of an event becomes so difficult that it is easier to describe it it terms of probability.

If 1,000,000 fair coins were flipped, probability states that 500,000 will land heads, and 500,000 will land tails. Although it is likely that this would not exactly happen, the true number of heads and tails will be close to this number. Thus, in events where the exact outcome is not easily determined, we use probability to approximate the outcome. So in reality, probability is a way for us to comprehend the outcome of something normally too complex for us to easily calculate.

Sample Size and Confidence Interval

It should be noted that the probability of a given event is not inherently known. It has to be calculated. Imagine that we do not know the probability that a fair coin will land heads, and are trying to calculate it. If the coin is flipped three times and lands heads twice, the only information that can be obtained is that heads has a 66% chance of appearing. To obtain an accurate probability of any given event, a large sample size is needed. If 100 coins are flipped, a possible result may be 55 heads. 55% is much closer to the "true" value than 66% is. In probability, there is something called the normal distribution, that describes the probability that any value lies within a certain number of standard deviations from the mean. The normal distribution is illustrated below.

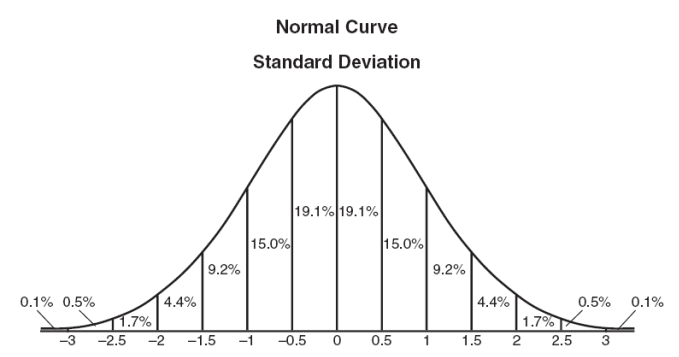
A table illustrating the normal distribution prepared by the NY State Education Department found at http://www.regentsprep.org/regents/math/algtrig/ats2/normallesson.htm

For example, there is a 68% chance that any given value lies within one standard deviation from the mean. However, this assumes an infinite sample size. In reality, no sample size is infinite. When dealing with a limited sample size, something called a confidence interval can be used to describe the confidence that the true mean lies within a certain value.

The equation for a confidence interval is a follows:

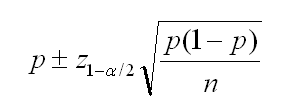
Confidence interval as described by Philip Mayfield retrieved from http://www.sigmazone.com/binomial_confidence_interval.htm

Where
p is the sample probability
n is the sample size
z_{1- α/2} is the confidence that you want, based on the normal distribution.
For example, in the example above where 56 heads were flipped, if you wanted to be 90% sure that the true value lies in a certain interval, you would calculate
0.55 ± 1.645 √(0.55(1-0.55)/(100)) = 0.55 ± 0.082
Having a higher confidence results in a wider range

For 95%,

0.55 ± 1.96 √(0.55(1-0.55)/(100)) = 0.55 ± 0.098

For 99%,

0.55 ± 2.57 √(0.55(1-0.55)/(100)) = 0.55 ± 0.128

Perhaps one of the most important things to take away from this equation is that increasing the sample size decreases the error.
If the sample size is increased from 100 to 1000, then the sample mean would likely be closer to the true value, and the error is decreased
An
If 512 coins out of 1000 land heads, and a 99% confidence interval is wanted, then

0.512 ± 2.57 √(0.55(1-0.55)/(1000)) = 0.512 ± 0.041
A much more accurate interval than the one calculated from the value calculated with only 100 trials.

An interesting consequence of the confidence interval is that given an interval, one can calculate the sample size they need to achieve that interval by rearranging the equation.

For a 99% confidence interval, if a interval of no more than 0.01 is wanted, than a sample size of 16500 is needed.

Is True Random Real?

So is there such a thing as true random? In short, no. Rolling a set of dice may seem random, but is in fact governed by physics. As you throw the dice, you put a torque and velocity on it. Afterwards, gravity takes over, causing the dice to fall a certain distance. As they hit they ground, they may roll or bonce, depending on the properties of the surface they are hitting. If the proper parameters were input to a computer, it could precisely calculate what the dice would land on every single time. Such a calculation for any single source of "randomness" could be developed.

In many cases, it is desirable to generate random numbers, however, computers cannot easily create random numbers.
Many computer applications use something called a pseudorandom number generator that takes an initial number called a seed, and preforms a complex algorithm on it to generate pseudo random numbers
below is a small example of what computers can do with random numbers. I made a program in which a number of boxes will appear. The boxes can randomly be brown, red, or grey, with red being the most common and grey the most rare. You can use the mouse to drag them around. If you drag them off of the screen, they will fall, and a new box will take its place in a random position on top of the screen.

However, no computer generated number is truly random, as is can always be traced back to its seed number from the algorithm.
The website random.org has a fairly unique solution to this problem. They generate random numbers based on background radio noise.

Some Examples

We can find many examples in nature where it is easiest to use probability to model what is happening. Any given event will most not likely not occur in the same way twice. For example, imagine if you were to take a cannon, launch it, and see where it lands. Consecutive cannons launched at the same velocity are likely to land in different spots. How the cannons land may look something like this.
target

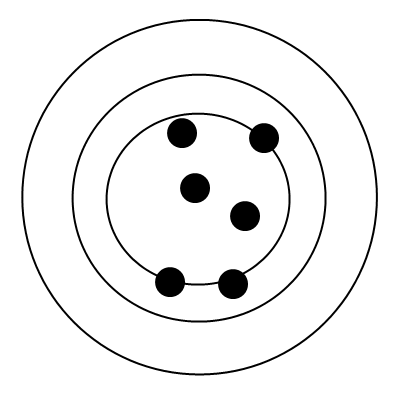
This image made by me illustrates possible landing spots of the cannon
Due to minor variations in the wind, shape of the projectile, and velocity, the cannon will most likely land in different spots.
Other examples of probability include radioactive decay and quantum theory.

Finding Life

"Space is big. You just won't believe how vastly, hugely, mind-bogglingly big it is. I mean, you may think it's a long was down the road to the chemist's, but that's just peanuts to space"
-Douglas Adams, The Hitchhiker's Guide to the Galaxy

The are lots of planets. As many as 100 billion [2] in our galaxy alone. Planets differ in many ways, from size to temperature, to the length of their days, to their composition, to many other things. Life needs a very specific type of planet to flourish. It can't be too hot, or too cold. The probability of these "perfect" condidions occuring is fairly low, but due to the sheer number of planets in existance, these planets may be fairly common. Astronomers have already discovered at least 29 planets within our own galaxy that may fit these criteria. Below is an artists representation of the planets ranked by distance from earth.

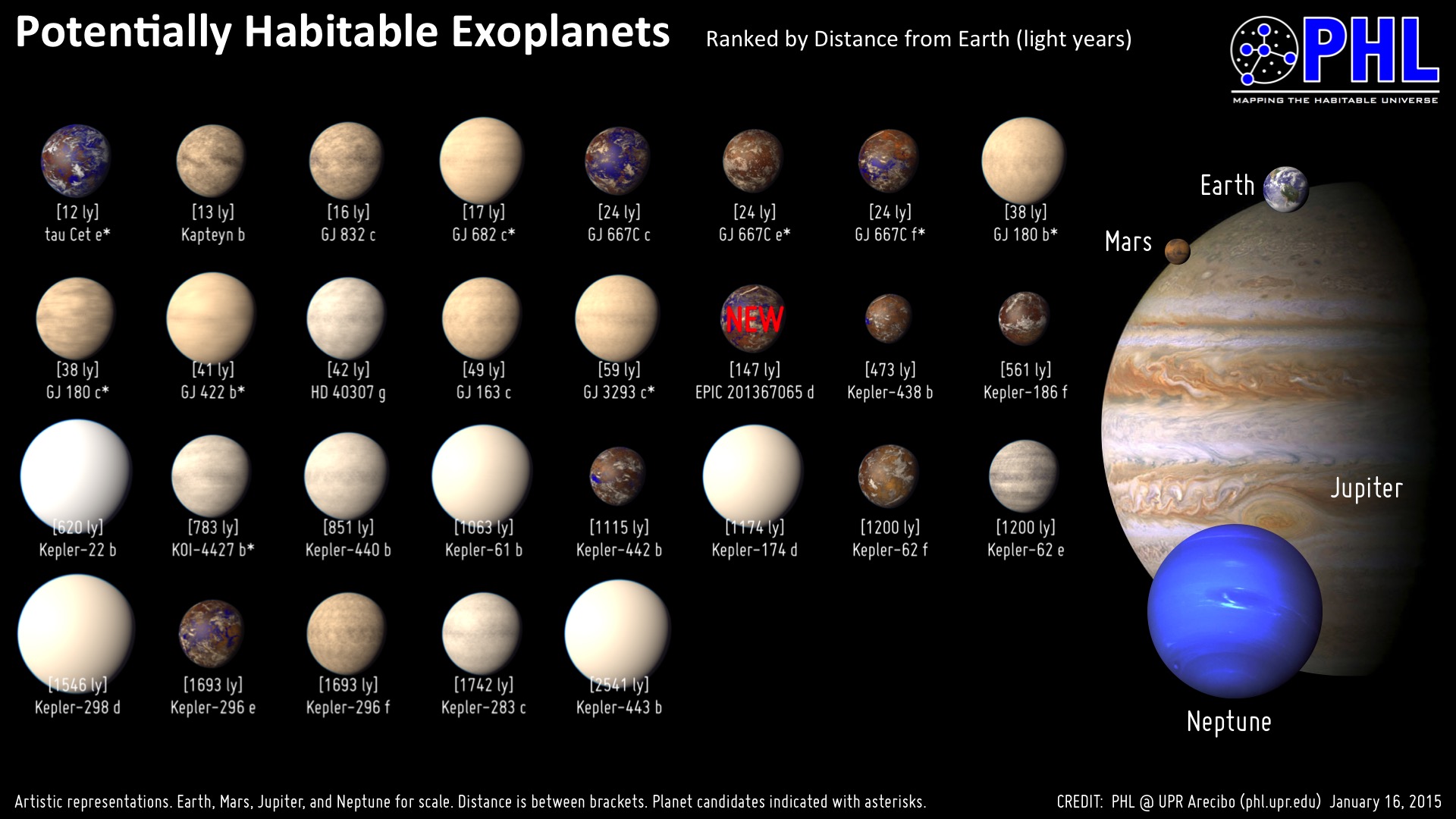
Planet By Distance

Image from (CC) Planetary Habitability Laboratory @ UPR Arecibo, 2015 found at http://phl.upr.edu/projects/habitable-exoplanets-catalog

So, what about life?
In 1961, Frank Drake presented what he called the "Drake Equation", an equation designed to calculate the what he believed would be the number of occurrences of intelligent life within the universe. The equation is

N = R_{\ast} \cdot f_p \cdot n_e \cdot f_{\ell} \cdot f_i \cdot f_c \cdot L

where:
N = the number of civilizations in our galaxy with which radio-communication might be possible

and
R_* = the average rate of star formation in our galaxy
f_p = the fraction of those stars that have planets
n_e = the average number of planets that can potentially support life per star that has planets
f_l = the fraction of planets that could support life that actually develop life at some point
f_i = the fraction of planets with life that actually go on to develop intelligent life (civilizations)
f_c = the fraction of civilizations that develop a technology that releases detectable signs of their existence into space
L = the length of time for which such civilizations release detectable signals into space

So, what is the result of this equation? The answer is that there's no good result. Many of the variables in this equation have to be estimated, so the equation gives us a fleeting glimpse at best. As the equation is filled in, the variables become harder to estimate. In particular, we have no idea how to estimate L, the length of time intelligent life may be able to broadcast. This is because we only have one example to compare to- ourselves. In 2010, the Italian astronomer Claudio
Maccone modified the drake equation to be represented as a log-normal distribution and developed the following graph

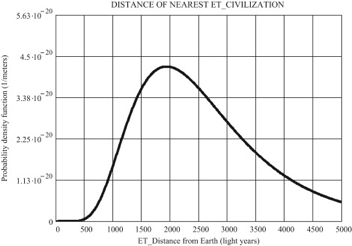
A bell curve demonstrating probability of finding nearby civilizations

This graph was created by Claudio Maccone in 2010

A link of his lecture can be found at
http://www.seti.org/seti-institute/weeky-lecture/statistical-drake-equation
With his equation, Maccone noted that there may be as many as 4,600 other civilizations in our galaxy alone.
He also noted that this is still a very rough guess, and that the number itself is not important.

The graph shows that the probability is almost zero at anything less than 500 light years. Humans started transmitting radio waves into space in the 1900's, so we haven't even transmitted 100 light years out yet.

Asteroid Impact

Another function of probability in physics is determining probability of asteroid impacts
NASA and other space monitoring agencies use something called the Torino Scale to measure the hazard of near Earth objects. The Torino Scale takes in account the probability of impact and the kinetic energy of the object to output an arbitrary danger scale.

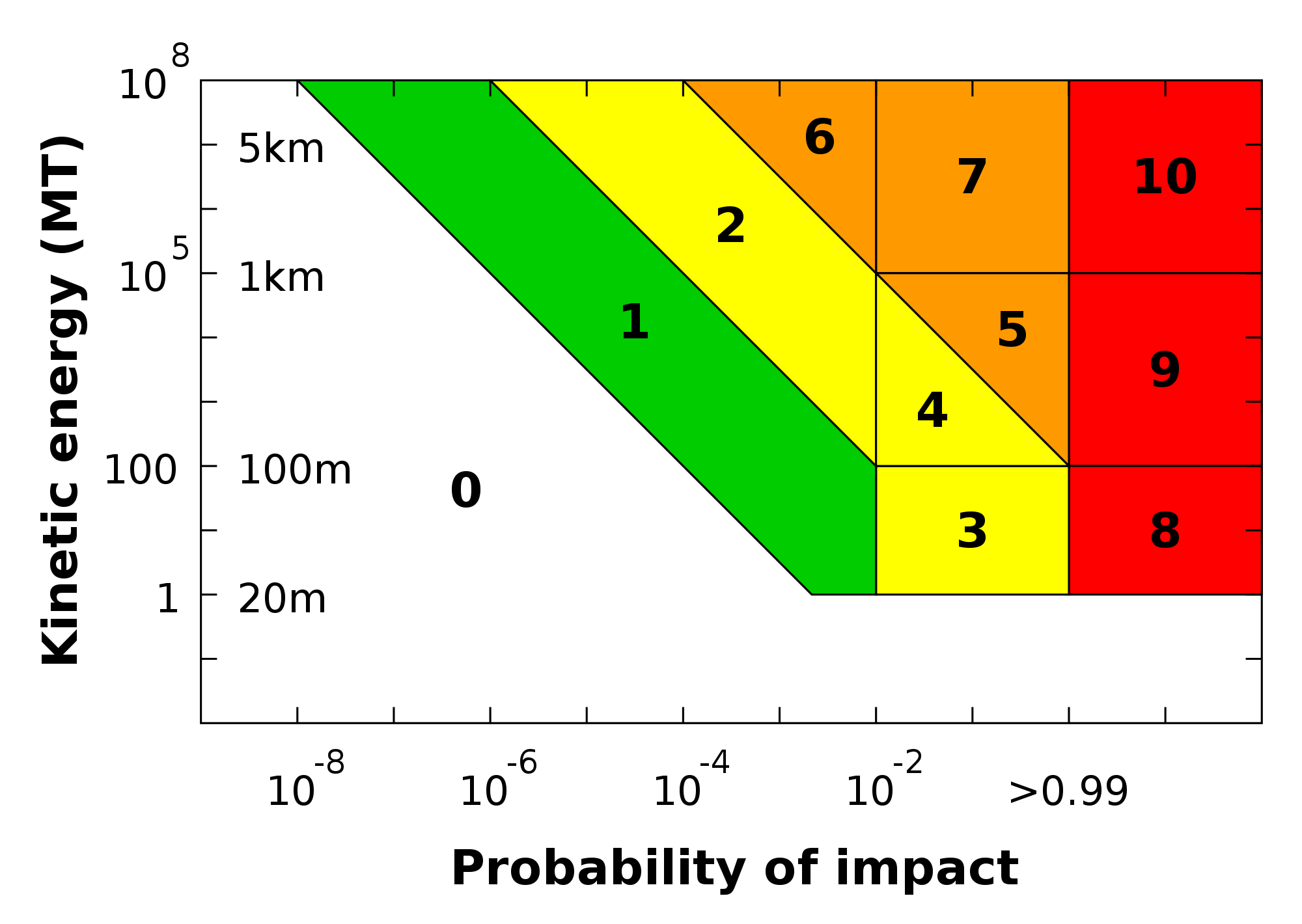
The Torino Scale as from http://impact.arc.nasa.gov/torino.cfm Image retrieved from http://en.wikipedia.org/wiki/Torino_scale

The NASA near Earth Object Program tracks hundreds of detectable asteroids, and has a database of asteroids that may impact Earth within the next 100 years. Currently, there are no objects with a Torino rating greater than 0.
The largest asteroid being observed is designated 29075 1950 DA. It is 1.3 km in diameter, and has been monitored since 1950. It is still a very low risk, as it only has a 1 in 20,000 chance of hitting sometime in the year 2800-2900.

Probability is an interesting concept. In reality, it is a way for us to represent something as absolute when we only have limited information on it. As we go towards the future, increasing sample size means that we will obtain increasingly accurate data that better allows us to understand our universe.

Bibliography
[1] Devore, J (2012) Probability and Statistics.San Luis Obispo, CA: Brooks/Cole Cengage Learning
[2]    100 Billion Alien Planets Fill Our Milky Way Galaxy. (2013) Space.com retrieved from http://www.space.com/19103-milky-way-100-billion-planets.html
[3]   Lewis, T (2013) Earth Like Planets Suprisingly Common In Huffington Post retrieved from http://www.huffingtonpost.com/2013/11/04/earth-like-habitable-planets-kepler-space-video_n_4214758.html
[4] The Drake Equation Frank Drake (1961) retrieved from http://www.seti.org/drakeequation
[5]    Habitable Exoplanet Catalog (2015) From The Planetary Habital Labratory retrieved from http://phl.upr.edu/projects/habitable-exoplanets-catalog
[6]     Haynes, W.M. (1996) CRC Handbook of Chemistry and Physics, 77th Edition
[7]     Earth Impact database (2011) From The Planetary and Space Science Centre, University of New Brunswick, Fredericton, New Brunswick, Canada retrieved from http://www.passc.net/EarthImpactDatabase/Diametersort.html
[8]    Risk Education (2012) From The institute of Materials, Minerals, and Mining retrieved from http://www.risk-ed.org/pages/risk/asteroid_prob.htm
[9]     Background courtesy of http://abstract.desktopnexus.com/wallpaper/1306989/, desktopnexus.com 2012
[10] Current Impact Risks (2015) NASA retrieved from http://neo.jpl.nasa.gov/risks/
[11]   How many alien civilizations are there? (2012) Bruno Martini retrieved from http://www.astrobio.net/news-exclusive/at-last-how-many-alien-civilizations-are-there/
[12]   Normal Distribution (2012) Donna Roberts retrieved from http://www.regentsprep.org/regents/math/algtrig/ats2/normallesson.htm
[13]   Understanding Binomial Confidence intervals (2013) Philip Mayfield retrieved from http://www.sigmazone.com/binomial_confidence_interval.htm