Propulsion: Wind, Force, and Work

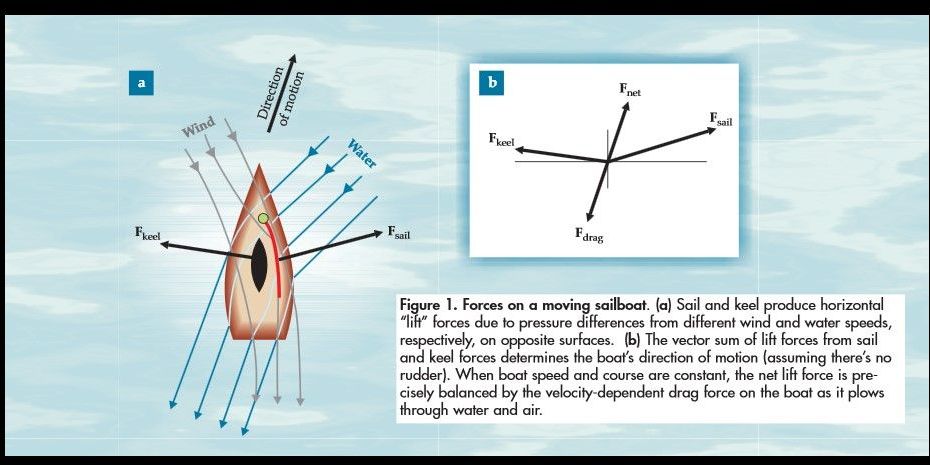
Sailing ships are propelled by various forces applied by the wind. Originally, ships could only travel when the wind was approaching their rear, or stern. This greatly limited the utility of older designs, leaving them completely at the mercy of shifting wind patterns. Later advancements in sail designs permitted ships to sail much closer to the wind utilizing an application of Bernoulli's Principle, more specifically, a "lift" force generated by a pressure differential. This difference in pressure is created by a difference in the velocities of fluids flowing across the sail. The sum of these "lift" forces generates an acceleration for the vessel dependent on its mass as dictated by Newton's 2nd Law, F = m x a.
Sails and Lift
Image Retrieved From:
http://www.sailingteam.tuc.gr/TUC_Sailing_Team/INTERESTING/Entries/2010/12/18_Physics_of_Sailing_files/PTO000038.pdf

Even with the discovery application of this ability to sail into the wind, it was still more effective to sail with the wind directly behind a ship. This may be demonstrated by calculating the work done on a ship by the wind. This may be modeled by the dot product of a constant force applied to the ship and the ship's displacement. This is given below. Note: Italicized letters represent vectors. For the purpose of this equation * represents the dot product, and theta is the angle between the vectors.

Work = F  * D = FDCos(theta)

If theta is zero degrees then cos(theta) = 1 and so the equation is maximized. This means that if the displacement vector and the force vector have the same bearing the work applied to the ship by the wind is at its maximum. As the units of work are the same as energy, conversion it may easily be transformed into kinetic energy, meaning that the ship's velocity would have increased as kinetic energy increased in magnitude.