Sound Waves To first truly understand the physics behind the guitar, we first need to establish a good basis on how waves work and how they relate to sound. Traveling waves come in two fundamental ways, transverse waves (like those seen on the string of a guitar) and longitudinal waves (these are the waves that produce sound). As just mentioned, sound is produced from longitudinal waves that create zones of varying pressures by compressing the air in front of them. 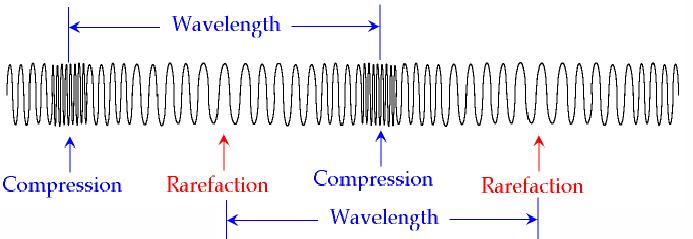https://www.boundless.com/physics/textbooks/boundless-physics-textbook/waves-and-vibrations-15/waves-125/longitudinal-waves-439-5596/ The picture above does a great job of depicting what a longitudinal wave looks like in free space by using a spring to represent the motion of the air particles. "In a longitudinal wave, the particles in the medium move parallel to the direction in which the wave travels" (Knight 561). In the picture above, this is represented by compression zones followed by zones of very low pressure (rarefaction zones) throughout the medium in which the wave travels. In the case of sound waves, the medium in which the wave propagates through is air. These compressions and rarefactions travel through the air and when they hit your ear drum, you hear the note played based on how many cycles per second there are, or the frequency of the wave. http://seekingintellect.com/2015/02/23/the-history-and-innovation-of-sound.html Lets take a look at some of the math involved: As a wave travels along, it moves with a certain velocity, v. As we know from basic kinematics, velocity=(distance)/(time). In the case with periodic waves, the distance is represented by the wavelength, denoted by the Greek letter lambda (λ). Another fundamental relationship that needs to be stated is that frequency=1/T, where T is the period of time it takes for the wave to travel one wavelength. By using this, we can see that v=λf. Another very important observation we need to make is by relating the above equation with vstring=sqrt(Ts/µ), where µ is the linear density of the string (µ=(mass)/(length)). By equating the two equations we have derived, we can solve for the frequency: f = (sqrt((TsL)/m)) / (λ) Guitar strings utilize these fundamental properties of waves to produce the correct pitch (frequency) of the desired note that is to be played. By looking at this equation, we can see that strings that are more massive result in much lower frequencies than less massive strings. This can easily be seen from the fact that the thicker more massive strings on a guitar produce the lower notes (notes with a low frequency). Also, strings that are under more tension will have higher frequencies than similar strings with less tension. On a guitar, as you tighten the tuning pegs, you are either putting that specific string under more or less tension and therefore changing the frequency produced by the string. This is how tuning pegs work on a guitar. http://www.wwk.in/physics/waves-and-optics