Determining the Shape of a Natural Balloon.
(the remnants of the balloon to the right are an example of crude balloon design.)
As is apparent, the balloon to the right is suffering a catastrophic failure. Sadly, this is the fate of just about every balloon that is let loose from fairs, playgrounds, and parks around the world. The balloon will rise and rise, until the surrounding pressure decreases to the point that the balloon expands and ruptures. Kind of cool, actually. This is why large atmospheric balloons appear to be under-inflated upon launch. As they rise, the gas inside starts to win the sumo wrestle with the atmosphere and achieves full inflation of the balloon.


during ascent and at design altitude, a balloon is subject to a cocktail of forces. If the forces are UN-evenly distributed in the balloon's film, localized stress will lead to envelope failure. While optimization of envelope shape may not be nessicary for a toy hot air balloon, it is quintessential when using light materials and lifting large loads! Almost all amateur balloon designs around today are based around the work of Justin Smalley.
....Enter Justin Smalley!
In the 1960s, a series of formal reports on the stress of every aspect of a balloon were produced by Justin Smalley. While his later reports delve into super pressure, unconventional balloon shape, and even the consideration of elasticity in the envelope material, his first two reports cover enough for the design of a hot air balloon. Below is a breif summary of what he did, A link to his complete works can be found under the links and references page.
First, Smalley finds the forces on the membrane.

Following, the forces are summed and an equation that describes the force on an area is produced.

The parameters of fabric weight, payload, and gas density difference are removed, and with an equation in hand, a calculation method is applied to use the Runge-Kutta method on a "high-speed" digital computer of the time.
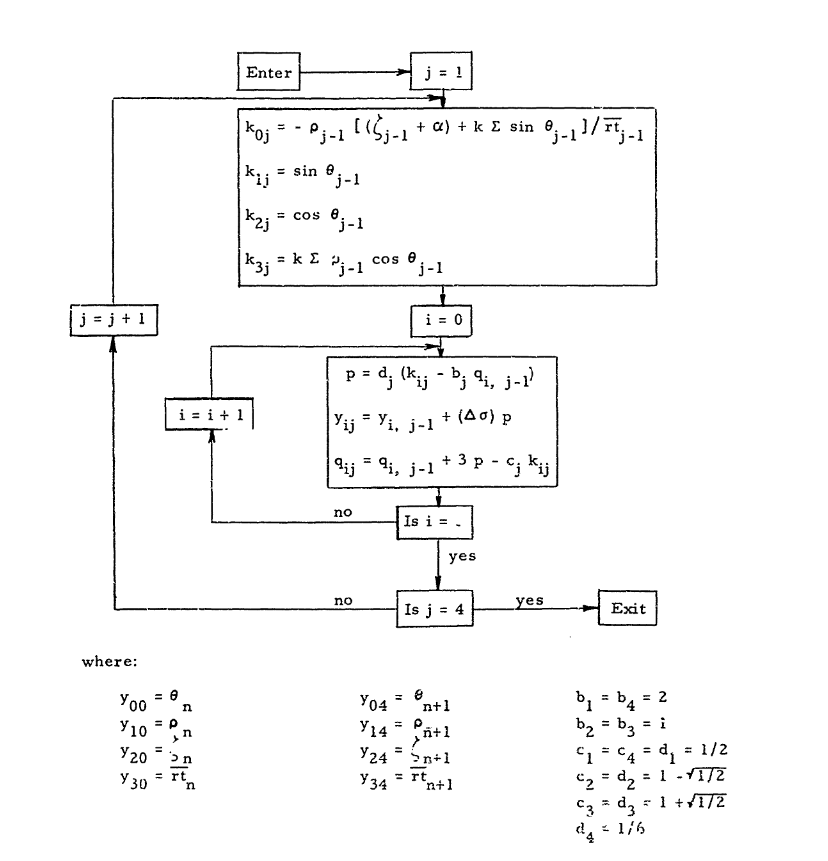
Derived are a table of values relating balloon measurements to varying gas density difference, balloon fabric material, and payload. These tables are referred to as "sigma tables" and the "sigma 0" table is the backbone of hot air balloon design today. A handful of ameature balloonists have produced excell-based balloon dimension calculation programs, but they are a nightmare to use and I recommend just reading Smalley's reports #1 and #2 to gain the knowledge to calculate your own balloon dimensions. I am no expert on the material they enclose, but the reports them self are an interesting genre of read.
As physical proof of this math working, here is a picture of a hot air balloon made of thin polyethylene sheet. This balloon was manufactured by Raven Industries in the mid 1960's, and achieved a gross lift of 450lbs. (1)
