In Alaska I find many winter outdoor enthusiasts have a preference: Snow machining, or snowboarding/skiing. Snow machining is fun, but I prefer snowboarding. The reason why is physics. With snow machining you become finely tuned with your machine. You learn terrain, and how your machine handles it, but, there is always that buffer of the heavy machine doing all the work. On a snowboard there is only a thin layer of board between you and the mountain. Gravity is your motor, and the only control you have is your posture, which allows you to shift your weight distribution over the board where your feet are bound to it. Whether you realize it or not everything you are doing is physics. Most experienced boarders learn from experience not experiments, but I aim to prove snowboarding is a bit of both.

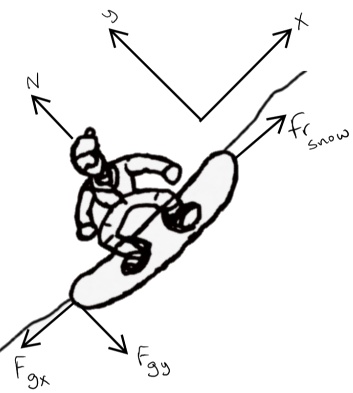
Let's start with the basics. Most resorts have a chairlift, Moose Mountain in Fairbanks uses a bus, alpine boarders may hike or even take a helicopter; fundamentally boarders transform some form of mechanical kinetic energy into potential energy. When standing atop a mountain covered in fresh powder there is nothing more fun than transforming that potential energy back into kinetic. Back to basics though, the first major hurdle all beginner snowboarders face is simply standing up. Take a look at the force diagram to the left to see why.
Common sense dictates you wouldn't start facing downhill, but that perspective makes it easy to draw in two dimensions. If it isn't obvious the x-axis is pointing straight uphill and the y-axis is perpendicular to the face of the mountain. No matter which direction you are pointed if you are standing with your board flat on the slope of the mountain these are the forces that will act on your center of mass. As you can see in the y-direction the normal force and the y-component of gravity counter each other. In the x-direction there are two unequal forces. Downhill in the negative x-direction is the x-component of gravity. To solve for this force we need the mass of our boarder, and the slope of our mountain. Lets say mass = 70 kgs and θ = 45°. Now using the approximate free-fall acceleration on earth g = -9.8 meters per second squared (Knight, 52) we can calculate the magnitude of the gravitational force vector: 70 kgs × -9.8 m/s² = -686 Newtons. To find the x-component of that gravity we simply take -686 N × sinθ ≅ -485 N.
This really tells us nothing though until we solve for the opposing force of friction.

It might not seem like snow should have friction, but consider solid objects on a microscopic level. Even seemingly smooth solids actually have small ridges, these ridges along with small electrostatic forces are what actually cause friction. Snow certainly has these ridges, just look at the expanded view of a snowflake to the right to see it's rigid design. These catch up on the small ridges on the bottom of a snowboard to cause friction. Some of this is counteracted by the force of your weight melting some of the snow which causes water to fill these ridges allow you to glide more freely. There are far too many variables to get into an extremely precise calculation of the coefficient of static friction between your board and the snow; for an example of just how many variables there are check out this guide on choosing wax racewax.com. An approximation is good enough for this small value though so I will use the value given from my textbook for the static coefficient of friction between wood and snow μ_s = 0.12 (Knight, 149). Now to find the frictional force all we have left to find is the normal force. The normal force as stated is just the opposite of the y-component of the gravitational force; which can be solved similarly to the x-component above: -686 N × cosθ ≅ -485 N. From here the friction force = μ_sN where N is the normal force (Knight, 148). μ_s × 485 N ≅ 58 N. So the sum of the x-component of the force of gravity and the friction force is -427 N, that is the force pulling you downhill. That's a very longwinded way of stating the obvious fact that you can't stand still on your board with your normal force perpendicular to the hill so let's make a comparison to get a better idea of just how little friction your board does have. The same frictional coefficients table used before states μ_s rubber on cement = 1.0. That means in work boots on a similar cement incline your static friction force would be 485 N. A little over 8 times the frictional force, and still right on the verge of sliding, the point being the snowboard does a very good job of reducing your friction against the mountain.

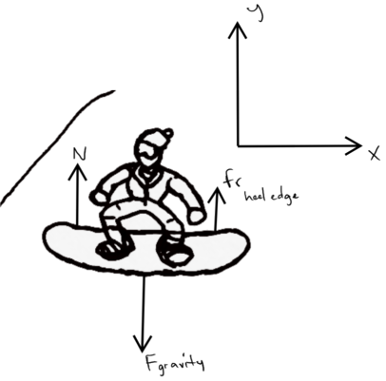
Back to our beginner - naturally rather than trying to stand facing down the mountain most would face perpendicular to the down direction. That would make you either directly facing towards or away from the mountain. As I stated before though the same force of gravity will pull down at your center of mass no matter which direction you face; and that is where shifting your weight comes into play. With rigid boots in rigid bindings you have basically two axes of control (not mentioning control you get from throwing around your momentum) which are the left foot right foot axis, and the heel toe axis. To stand up you need to have your left/right axis balanced, but most importantly you need to lean into either your toe axis if you are facing the mountain or your heel axis if you are facing away. What this does is levels your board, you want the plane of your board to be level. In doing so rather than putting the smooth surface under your board on the slippery snow you are digging the sharp metal edge right into the mountain. Also you are making your normal force parallel to the force of gravity; it takes practice, at first it can seem like trying to stand on a couple of bars of soap in the shower, but to get anywhere you need to get comfortable standing in place. Not just for standing, this is also how you stop. To the left is a force diagram of our boarder standing still on his heel edge. The y-axis is pointing straight up, not the slope of the mountain, and the forces are all parallel to the y-axis. From this stance many beginners learn to lean towards the slope of the mountain just enough to do slowly, plowing the snow; it is known as "The falling leaf" and many other names. Now that we've gone over the basics let's get things going on my next page KINETIC.

References