Several photos were taken of levitating tables in the séances with Miss Goligher, but I note that all of them show the table with at least one leg (and normally two) on the floor. For the purposes of this project, I make a distinction between a table that is fully lifted from the floor and one that is tilted to one side. More discussion will follow in the section where I get to the math of the matter!

from http://felixcircle.blogspot.com/2013_03_07_archive.html

Force needed for such phenomena (where the Physics starts!)

If we take a structure such as the basic cantilever design (which is connected at one end to the medium and at the other to the table), the force needed to actually lift a table will be a function of the length of the cantilever and the mass of the table. The force applied at the underside of the table will have to match the force due to gravity.

And if we take the cantilever design as the most functional of Crawford's proposed lifting structures, there needs to be an upward force applied somewhere along the lever such that the following equivalence can be found:

F1D1=GD2

Where F1 is the lifting force closer to the medium, G is the actual weight of the table, and D1 and D2 are the distances of each along the cantilever arm from the anchor point at the medium.

Since the moment of rotation will be at the anchor to the medium, the lifting force will have to be significantly greater than the weight of the table, which will also be magnified along the arm of the cantilever.

A picture may help:

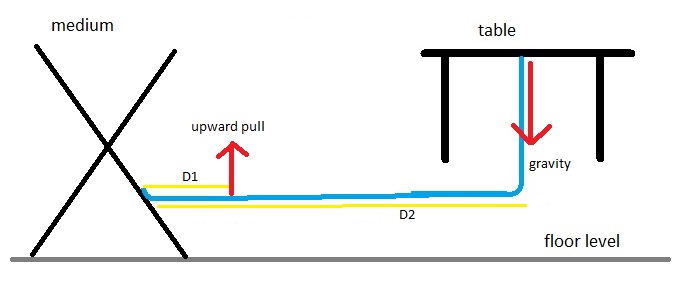
For simple understanding, assume the length of the cantilever arm to be 1 meter. With a mass of say 6.44 kg, the table exerts a moment of 63.2 Nm at the anchor of the cantilever.

Now, assume the upward force is at 0.5 meter. In order to lift the table, the force will have to be exactly double the downward gravitational force. So, if D1 = 0.5D2, F1 has to be 2G.

The upward force to lift the table, if applied at half the length of the moment arm, will be twice the weight of the table.  And the shorter the distance from the medium to the upward force, the greater that force has to be. 

Even a small table may get rather difficult to lift with such a structure, depending on exactly where the force is applied!  With my experimental table, this would require an upward pull of 126 Newtons, which is fairly significant. More on this in the next section.

I suppose one could posit a force applied to the cantilever arm closer to the table, which would mean a smaller force, but at no time can the force be less than the weight of the table.

Suppositional Alternative Application of Force

In order to merely tip the table, as all of the photographs of the phenomena with Miss Goligher actually show, a much smaller force can be applied at a distance from the center of mass of the table and result in movement and lifting of one side of the table.