Gravity Without gravity, powerlifting wouldn't be possible. The entire concept behind the sport revolves around exerting a force on a given mass in order to move it a distance until the point of lock out which will be explained on each individual lift. Since powerlifting events take place on Earth and we know the acceleration of Earths gravity, the famous formula of Newton's second law can be used: F=ma. Ex: Lifter A has to lift 300 kg in one of the three lifts. Since a= 9.81 (m/s^2) F = (300 kg) (9.81m/s^2) = 2940 N Therefore Lifter A must exert more than 2940 Newtons of force to move the weight upward. Forces                           All forces experienced by the lifters body are due to gravity. Gravity applies a downward linear force on the lifter, and the lifter applies a force in the opposite direction to prevent the weight from accelerating to the ground at 9.81 m/s^2. When the weight is stationary and is not in motion, the force being applied by the lifter is the normal force. If the weight is descending, the applied force is smaller than that of the gravitational force. If the weight is ascending, the lifter is supplying a force greater than that of the force from the weights. From the perspective of biomechanics, forces in joints and on different bones vary. Different stances or grips can make the lift easier or harder. This is discussed in detail on each of the individual lifts.    Moments 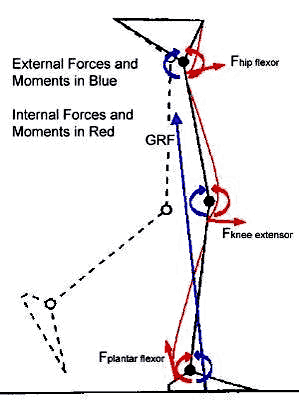   Moments also play a very big role in powerlifting. Moments are created in joints like the knees, hips, ankles, elbows, and shoulders. The magnitude of the moment varies at different stages of the movement. For example, the moment about the knee is greatest when the lifters femur is perpendicular to the ground because the entire vertical load of the weight is farthest from the knee. Using the equation Moment = Force x Distance would be used in determining the magnitude of the force. Since the equation involves a cross product, a perpendicular load results in the greatest force. f   Work In addition to forces and moments, work done on gravity can also be calculated in all three lifts. In a lift like the dead lift, a weight is moved from one height to another meaning that the potential energy of the weight changes. This change can be calculated using the equation Work = (Force)(Distance). Ex: Lifter B performs the dead lift with 200 kg. he lifts the weight a total height of 0.4 meters. The potential energy gained can be calculated as follows: W = (F)(D) F = (200 kg)(9.81m/s^2) =  1,962 N W = (1962 N)(0.4 m) = 784.8 J