You may have noticed that we really don't know much about the craft's actual construction so it is difficult to say exactly what it would take to sink one. However, we do know that because the rowers are positioned below the upper deck and that there were likely mutiple levels of them, that at some point our boat would begin shipping water through the oar windows once it dropped a certain distance below water.

    But what IS that distance? We can't really know for sure, but we can guess and find the angle of the boat at its equilibrium when a certain portion of it is submerged.

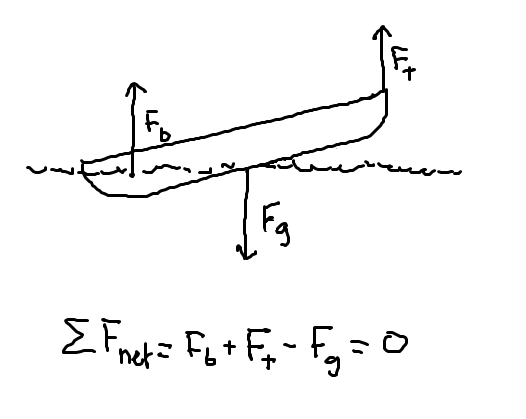
    Here we see our boat at equilibrium where the force of tension and bouyancy balance out the downward force of gravity which we calculated before to be about 1,887,914.443 Newtons. Remembering Archimedes principle of bouyancy, which states that the bouyant force is equal to the weight of the fluid that the body displaces, or, 

F = (rho)(gravity)(volume)

    We know that as our boat is levered out of the water the bouyant force will get smaller and smaller as the area submerged gets smaller and smaller. This means that with a constant force of tension the other end of the boat will sink lower and lower under water before equilibrium is reached.

    But how can we figure out how much volume is displaced? At any given time while the boat it is floating on the surface of the water, 192,644.33 Newtons is equal to gravity times the volume of water displaced times acceleration due to gravity times the density of water, (about 1022 kilograms per cubic meter.)

    Simplifying and solving for the volume we get ...

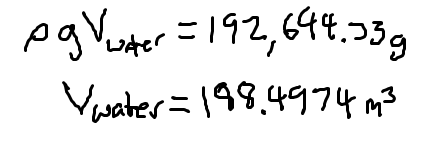
    About 188.5 cubic meters. That's about 67 percent of the volume of our boat. But then again, we only found the volume of the walls and hull and deck. Remember, it is mostly hollow on the inside so to find the volume of water it really displaces we need to find the total area the boat takes up. Going back to our diagram from earlier we find that...

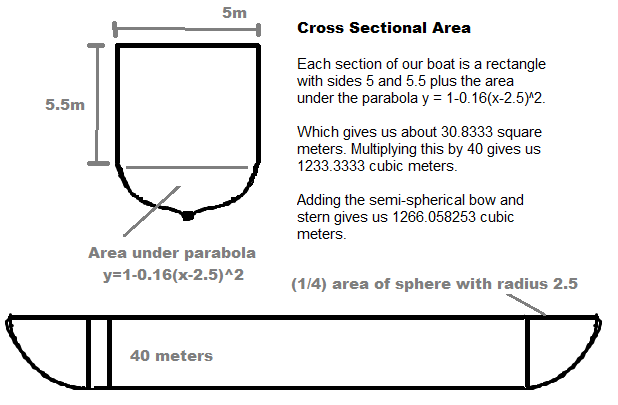
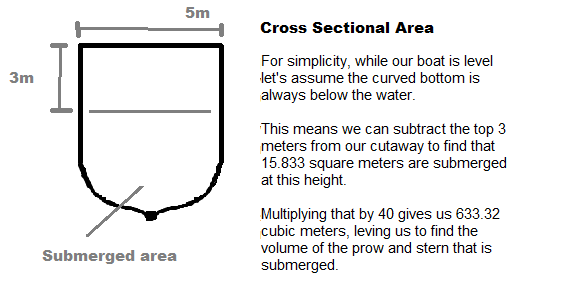
    So our boat actually displaces about to 1266 cubic meters of water. That's a potential bouyant force of up to 12,680,333.04 Newtons! This also means that only roughly one seventh of the boat needs to be submerged while it's level, meaning it's probably still a little too light. Remember, Polybius told us that they floated about 3 meters above the water.
 
    This should be expected though considering that ours still has no ballast, mast, sails, or other items like armor and weapons that the Romans would likely have on board. It is also worth noting that the quinqueremes we are concerned with would have also had siege towers and sambucas on them, making them even heavier.

    For the sake of historicity let's find the actual weight we would need to be exactly 3 meters above the water.

    The bow and stern in our model are both semi-spheres which means we will need to integrate the equation for a sphere to find an equation for height.

   Plugging in our height, (beneath the water, so 3.5, not 3,) gives us 11.91187. Multiplying that by two and adding it to our other value gives us 657.1437 cubic meters. Multiplying by the density of water gives us 671600.814 kilograms.

    This means, if the dimensions given to us are accurate, our boat would have to rise only 3 meters above the water it would have to weigh approximately three and a half times what it currently does.

    With this weight let us find the angle (theta) at which the boat is at equilibrium and its entire stern is below the water.

    Of course, we don't know for sure if the boat will sink at this point, but you could reasonably suspect that water would begin pouring in through the oar slots near the back of the boat, while those in the front and back would be unable to propel the ship effectively, many of the oars being too far above the water and many below it.

   
    Dropping the boat from this height as Polybius describes may not even have been necessary as the crew would be helpless to do much other than bail water. It is however worth noting that if we had stuck with our much lighter quinquereme doing the same calculations again would give us an angle of 33.55 degrees.