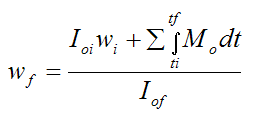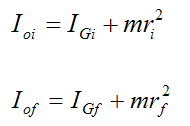The physics of skating on a half-pipe:
Energy is neither created nor destroyed. When skating a half-pipe, you are illustrating just that. When you are at the top of the half-pipe, you possess gravitational potential energy, and while you are moving, you gain kinetic energy. Using the equation below, you can calculate the total mechanical energy that you have while skating on a half-pipe. Total mechanical energy equals to your gravitational potential plus kinetic energy. To find your gravitational energy, multiply your mass, by earth's gravitational energy 9.81 m/s^2 and your height on half-pipe (in meters). To find your kinetic energy, multiply your mass, by 1/2 and your speed squared. Your potential energy should be equal to your kinetic energy, but energy can be lost through friction, from noise due to your skateboard against the pavement, and heat due to friction.
The Physics of Pumping on a half-pipe:
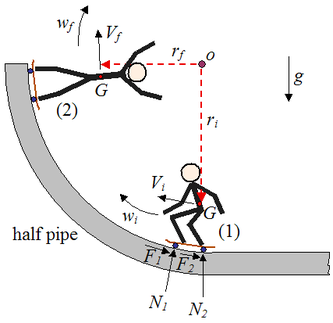
On a half-pipe, a skater is not only limited to just skating up and down, but a skateboarder can also use a half-pipe to gain vertical speed and to do mid-air tricks. In this case, the skater's feet doesn't leave the board, at all. In this case, the skater uses the physics of angular impulse and momentum. Using the diagram below, I will explain to you how this works.
 http://www.real-world-physics-problems.com/physics-of-skateboarding.html
http://www.real-world-physics-problems.com/physics-of-skateboarding.html
Since we are on earth, gravity always wants to bring us down which is represented as g. Which causes the normal forces N_1 and N_2 on the wheels of the skateboard. At position 1, w_i is the initial angular velocity acting on the system (the skater and the skateboard). V_i is the initial velocity of the skater at position 1. F_1 and F_2 are the frictional forces acting on each wheel. r_i is the initial distance to the center of rotation, O, to the center of mass of the skater which is represented here as H. At position w_f is the final angular velocity of the skater, V_f is the final velocity and r_f is the final distance to the center of rotation, O, to the center of mass, G.
Given the first equation on the left, we can find the skater's final angular velocity, W_f. In this equation I_oi is the initial moment of the inertia acting on the skater and I_of is the final moment of inertia. W_f is equal to the initial moment of inertia multiplied by the initial angular velocity added to the sum moments of inertia on the skater's body divided by their final moment of inertia.
Using the equation on the right, we can find the initial and final moments of inertia, where I_Gi is the moment of inertia of the body passing through point G and out towards you on position 1 (the reader) and I_Gf is the moment of inertia of the body passing through point G and towards you at position 2 where m stands for the skater's mass in both cases. If you decrease the I_of you will increase w_f, to do this the skater would have to make their center of mass smaller at point o.
The skater can increase their velocity by crouching down and lifting their arms up while on the concave part of the half-pipe while the skater is doing this, they will feel like their arms want to move away from their center of rotation, o this is due to the centripetal acceleration force.
Using the equation on the right, we can find the initial and final moments of inertia, where I_Gi is the moment of inertia of the body passing through point G and out towards you on position 1 (the reader) and I_Gf is the moment of inertia of the body passing through point G and towards you at position 2 where m stands for the skater's mass in both cases. If you decrease the I_of you will increase w_f, to do this the skater would have to make their center of mass smaller at point o.
The skater can increase their velocity by crouching down and lifting their arms up while on the concave part of the half-pipe while the skater is doing this, they will feel like their arms want to move away from their center of rotation, o this is due to the centripetal acceleration force.