Distance

Bullseye

Source: http://spectre23.wordpress.com/2009/08/23/sw-22a-shoots-like-a-champ/

Home

Wind

Bibliography

Distance can have many different affects on the ballistics of a bullet, chiefly among those is bullet drop. The longer a bullet travels through the air the more time every element that opposes its motion is able to act on it. These include gyroscopic drift, wind, and air density. An example of a situation where distance is accounted for can be easily found using the kinematic equations as shown below. Understand that this example ignores all of the elements that oppose the motion of a bullet except for distance and gravity.
Slowmo

For the following example the starting position will be at zero meters with a barrel angle of zero degrees (parallel to the ground) that is 2 meters above the ground. The starting velocity will be 599.84 meters/second which is the velocity of a 30-06 round with a powder load of 40 grains using smokeless powder. The final velocity for this example will be zero (bullet hits the ground).

The equations that will be used for this example are called the kinematic equations for projectile motion. (shown below)
The second equation will be used to find the time it will take for the bullet to hit the ground. This equation will be used in the y direction.
We will then use the same equation to find the distance the bullet travels (x final). This equation will be used in the x direction.

Source: http://spi4uk.itvnet.lv/upload/articles/45/450133/images/_origin_Zirnekla-cilveki-8.jpg

First step using the second equation in the y direction: 0m=2m+(1/2)*9.81(m/s^2)*t^2 to find that t=0.639 seconds
Second step using the time found in step one combined with the second equation to find the distance the bullet will travel:
x(final)=0m+599.84(m/s)*0.639s+(1/2)*0(m/s^2)*0.639s^2 since the acceleration and initial position is 0 we find that x(final)= 599.84(m/s)*0.639s
From this we know the distance a bullet will travel with an initial muzzle velocity of 599.84 meters per second at a height of 2m is 383.03 meters.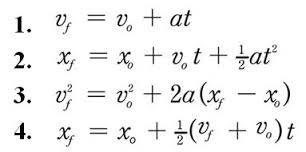

Equations

Source: https://www.teachengineering.org/collection/nyu_/activities/nyu_projectile/nyu_projectile_activity1_image2.gif

This example demonstrates how far a bullet can travel while not under any factors that may slow it down. The factors that do affect a bullets trajectory under real world conditions will be discussed in the following pages.